Эффект Арки: Приложения. Куски программы.

Это страница, объясняющая принцип построения программы http://darkenergy.narod.ru/arcru.exe Модели Звезд, exe-файл, для решения системы дифференциальных уравнений, описывающих поведение физических величин в недрах гравитирующих объектов. Этот текст был написан в 2003 году. С тех пор программа была неоднократно усовершенствована, но сам принцип и главные выводы остались прежними.

Программа для идеального газового объекта без оболочки, записанная в Visual Basic.

Для объекта без оболочки работает система уравнений:

dp/dr = - gmn + 2p/r. (1)
dn/dr = 2n/r - gn/v². (2)
dT/dr = - (2/3)mg/k. (3)
dM/dr = 4pr²mn. (4)
g = GM/r². (5)
p=nkT. (6)

Уравнение (3) в программе будет записано в виде: T(i) = T(i - 1) + mat * g(i) / kB * dr * (2 / 3). Этот вид подучен заменой dT=T(i-1)-T(i). Первое слагаемое содержит индекс (i-1), второе (i). Это объясняется тем, что первый слой у нас на поверхности, и нумерация слоев идет к центру объекта.

Уравнение (2) в программе будет записано виде: n(i) = n(i - 1) - (2 * n(i - 1) / R(i) - g(i) * n(i - 1) * mat / 3 / kB / T(i)) * dr. Этот вид получен заменой dn = n(i-1)-n(i).

Давление в программе можно определять по одной из формул: либо (1), либо (5).

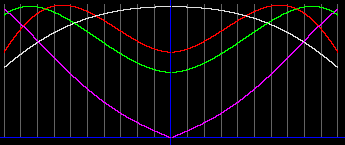
В результате выполнения программы будут построены графики:

Белая линия - температура, красная - давление, зеленая - концентрация частиц, желтая - масса объекта под радиусом r.

На экран будут выведены результаты, подтверждающие то, что в данном объекте работают законы термодинамики, и расширенная теорема о вириале.

Dim k, E, A, Ek, Ep, GN, pi, kB, dr, mat, dEk(30000), dEp(30000), dA(30000), dM(30000), M(30000), p(30000), n(30000), T(30000), R(30000), g(30000)
AutoRedraw = 1
RESULT4.Visible = True
DrawWidth = 2
pi = 4 * Atn(1)
GN = 6.67259E-11 'Гравитационная константа
c = CDbl(299792458) 'скорость света
kB = 1.3806503E-23 ' постоянная Больцмана
mat = 2 * 1.66053873E-27 'масса частицы
For i = -2 To 18 'рисуем систему координат
Line (2000 + 500 * i, 2000)-(2000 + 500 * i, 6000), RGB(100, 100, 100)
Next
Line (0, 6000)-(12120, 6000), RGB(0, 0, 256)
Line (6000, 200)-(6000, 9120), RGB(0, 0, 256)

M(0) = 1.9891E+30 'масса объекта.
R(0) = 696100000# 'радиус объекта
dr = R(0) / 30000 'толщина слоя
g(0) = M(0) * GN / R(0) ^ 2 'ускорение g на поверхности объекта
R(1) = R(0) - dr 'радиус объекта под 1-ым слоем.
M(1) = g(0) * R(1) ^ 2 / GN 'масса объекта под радиусом Rob - dr.
dM(1) = M(0) - M(1) 'масса объекта над радиусом Rob - dr.

'Определяем коэффициент k, который войдет в формулу для давления p(1).
'Подбираем его, прогоняя программу
'пока не будут выполняться условия в центре: M=0 при r=0.
k = 1.02169307106754

'эмпирическая формула для вычисления давления в первом слое.
p(1) = k * GN * M(0) ^ 2 * R(0) ^ (-15 / 2) * R(1) ^ 2 * (R(0) - R(1)) ^ (3 / 2)
'формула для вычисления температуры в первом слое.
T(1) = (2 / 3) * GN * M(0) * mat * dr / kB / R(0) ^ 2
'концентрация частиц в первом слое.
n(1) = p(1) / kB / T(1)
'потенциальная энергия первого слоя
dEp(1) = -GN * M(1) * dM(1) / R(1)
'кинетическая энергия первого слоя
dEk(1) = (3 / 2) * p(1) * 4 * pi * R(1) ^ 2 * dr
'работа по сжатию первого слоя
dA(1) = p(1) * 4 * pi * R(1) ^ 2 * dr

'вычисляем значения физических величин послойно,
'и некоторые из них суммируем
For i = 2 To 29999
' идем вглубь с шагом dr
R(i) = R(i - 1) - dr
' масса над i-тым слоем равна массе над слоем i-1 плюс масса i-того слоя
dM(i) = dM(i - 1) + 4 * pi * R(i) ^ 2 * n(i - 1) * mat * dr
'масса под i-тым слоем.
M(i) = M(0) - dM(i)
' ускорение g i-того слоя.
g(i) = GN * M(i) / R(i) ^ 2
' температура i-того слоя по формуле (2).
T(i) = T(i - 1) + mat * g(i) / kB * dr * (2 / 3)
' концентрация в i-том слое по формуле (3)
n(i) = n(i - 1) - (2 * n(i - 1) / R(i) - g(i) * n(i - 1) * mat / 3 / kB / T(i)) * dr
' давление в i-том слое по формуле p=nkT или(1).
p(i) = n(i) * kB * T(i) 'или: p(i) = p(i - 1) - (-mat * n(i) * g(i) + 2 * p(i - 1) / R(i)) * dr
' суммируем потенциальную энергию слоев
dEp(i) = dEp(i - 1) - GN * M(i) * (dM(i) - dM(i - 1)) / R(i)
' суммируем кинетическую энергию слоев
dEk(i) = dEk(i - 1) + (3 / 2) * p(i) * 4 * pi * R(i) ^ 2 * dr
' суммируем работу по сжатию газа в слои
dA(i) = dA(i - 1) + p(i) * 4 * pi * R(i) ^ 2 * dr
Next

'Строим графики функций
For i = 2 To 29990
X = 1000 + i * (0.5) / 3
x1 = X + (0.5) / 3

'масса объекта под радиусом rr(i)
y = 6000 - M(i) / 5E+26
y1 = 6000 - M(i - 1) / 5E+26
Line (X, y)-(x1, y1), RGB(200, 235, 0)

'давление в i-том слое
y = 6000 - p(i) / 13000000000#
y1 = 6000 - p(i + 1) / 13000000000#
Line (X, y)-(x1, y1), RGB(255, 0, 0)

'концентрация в i-том слое
y = 6000 - n(i) / 1.4E+26
y1 = 6000 - n(i + 1) / 1.4E+26
Line (X, y)-(x1, y1), RGB(0, 255, 0)

'температура в i-том слое
y = 6000 - T(i) / 2900
y1 = 6000 - T(i + 1) / 2900
Line (X, y)-(x1, y1), RGB(220, 220, 220)

'ускорение g в i-том слое
y = 6000 - g(i) * 13
y1 = 6000 - g(i + 1) * 13
Line (X, y)-(x1, y1), RGB(225, 0, 255)

' красивая кривая к теореме о вириале
y = 6000 - ((3 / 10) * g(i) * R(i) ^ 3 * n(i) * mat * dr - R(i) ^ 3 / 2 * (p(i) - p(i - 1))) / 3E+32
y1 = 6000 - ((3 / 10) * g(i + 1) * R(i + 1) ^ 3 * n(i + 1) * mat * dr - R(i + 1) ^ 3 / 2 * (p(i + 1) - p(i))) / 3E+32
Line (X, y)-(x1, y1), RGB(100, 100, 100)
y = 6000 - ((1 / 5) * g(i) * R(i) ^ 3 * n(i) * mat * dr - R(i) ^ 2 * p(i) * dr) / 3E+32
y1 = 6000 - ((1 / 5) * g(i + 1) * R(i + 1) ^ 3 * n(i + 1) * mat * dr - R(i + 1) ^ 2 * p(i + 1) * dr) / 3E+32
Line (X, y)-(x1, y1), RGB(100, 100, 100)

'Комбинация величин, выраженная в единицах энергии,
'получена для сравнения с другими величинами.

Ek = dEk(29999) 'кинетическая энергия всех частиц объекта
Ep = dEp(29999) 'потенциальная энергия всех частиц объекта
A = dA(29999) 'работа по сжатию объекта
'вывод на экран интересных отношений
RESULT4 = RESULT4 & " Ek=" & Ek & " Ep=" & Ep & " A=" & A & " Ratio1=" & -Ep / (A + Ek) / 2 & " (2/3)Ek/A=" & (2 / 3) * Ek / A & " E=" & E & " Ep/E=" & Ep / E & " Ratio2=" & E / (Ep - Ek - A)
SavePicture Image, "radiation.bmp"

В окне "result4" появятся результаты
Ek=6,69164125355022E+40
Ep=-2,23075339939276E+41
A=4,46109416903349E+40
Virial=1,00009249518984
T-dynamic=1,00000002980232

Результат T-dynamic=1,00000002980232 показывает, что законы термодинамики работают: U=3/2RT, A=RT, (2/3)Ek/A=(2/3)U/A. (Хвост ...02980232 - артефакт; в других задачах до конца идут нули, или девятки.)

Результат RatioVirial=1,00009249518984 показывает, что работает РАСШИРЕННАЯ теорема о вириале: Ep=-2(A+Ek). Количество нулей перед хвостом ...09249518984 зависит от того на сколько слоев мы разбиваем объект. Чем больше слоев, тем результат ближе к единице. См. Эффект Арки и теорема о вириале

Программа для идеального газового объекта, зажатого в оболочке

В отличие от задачи выше, для объекта, зажатого в оболочке, в уравнении (1) добавляется слагаемое p₀, означающее давление оболочки на газ, и преобразуется уравнение (2) в соответствии с уравнениями (1, 3, 6).

dp/dr = - gmn + 2(p-p₀)/r. (1)
dn/dr = 2n/r - gn/v² - 2np₀ / pr. (2)
dT/dr = - (2/3)mg/k. (3)
dM/dr = 4pr²mn (4)
g = GM/r². (5)
p=nkT. (6)

В результате выполнения программы будут построены графики:

Dim dr, pi, mat, kB, GN, M(30000), dEk(30000), dEp(30000), dA(30000), dM(30000), p(30000), n(30000), T(30000), R(30000), g(30000), pshell
AutoRedraw = 1
RESULT4.Visible = True
DrawWidth = 1
pi = 4 * Atn(1)
GN = 6.67259E-11 'Гравитационная константа
kB = 1.3806503E-23 ' постоянная Больцмана
mat = 29 * 1.66053873E-27 'масса частицы

For i = -2 To 18 'рисуем систему координат
Line (2000 + 500 * i, 2000)-(2000 + 500 * i, 6000), RGB(100, 100, 100)
Next
Line (0, 6000)-(12120, 6000), RGB(0, 0, 256)
Line (6000, 200)-(6000, 9120), RGB(0, 0, 256)

'Произвольно зададаем температуру оболочки, массу газа в оболочке, радиус оболочки.
T(0) = 100
M(0) = 8.382E+21
R(0) = 6370000
dr = R(0) / 30000 'Толщина слоя

'Методом последовательного приближения подбираем давление газа
'в первом слое таким, чтобы соблюдались условия в центре: M(i)=0 при(R=0).
p(0) = 223252.662694055

n(0) = p(0) / kB / T(0) 'Концентрация частиц газа возле оболочки.
g(0) = M(0) * GN / R(0) ^ 2 'Ускорение g возле оболочки.

'Вычисляем значения физических величин послойно и некоторые из них суммируем
For i = 1 To 30000
R(i) = R(i - 1) - dr
dM(i) = dM(i - 1) + 4 * pi * R(i) ^ 2 * n(i - 1) * mat * dr
M(i) = M(0) - dM(i)
g(i) = GN * M(i) / R(i) ^ 2
T(i) = T(i - 1) + mat * g(i) / kB * dr * (2 / 3)
n(i) = n(i - 1) - (2 * n(i - 1) / R(i) - g(i) * n(i - 1) * mat / 3 / kB / T(i) - 2 * n(i - 1) * p(0) / p(i - 1) / R(i)) * dr
p(i) = n(i) * T(i) * kB
dEp(i) = dEp(i - 1) - GN * M(i) * (dM(i) - dM(i - 1)) / R(i)
dEk(i) = dEk(i - 1) + (3 / 2) * p(i) * 4 * pi * R(i) ^ 2 * dr
dA(i) = dA(i - 1) + p(i) * 4 * pi * R(i) ^ 2 * dr
Next

'Строим графики функций
For i = 1 To 29998
X = 1000 + i * (0.5) / 3
x1 = X + (0.5) / 3

'масса объекта под радиусом r(i)
y = 6000 - M(i) / 2.1E+18
y1 = 6000 - M(i + 1) / 2.1E+18
Line (X, y)-(x1, y1), RGB(200, 235, 0)

'давление в i-том слое
y = 6000 - p(i) / 87
y1 = 6000 - p(i - 1) / 87
Line (X, y)-(x1, y1), RGB(255, 0, 0)

'концентрация в i-том слое
y = 6000 - n(i) / 4.4E+22
y1 = 6000 - n(i + 1) / 4.4E+22
Line (X, y)-(x1, y1), RGB(0, 255, 0)

'температура в i-том слое
y = 6000 - T(i) * 21
y1 = 6000 - T(i + 1) * 21
Line (X, y)-(x1, y1), RGB(220, 220, 220)

'ускорение g в i-том слое
y = 6000 - g(i) * 280000
y1 = 6000 - g(i + 1) * 280000
Line (X, y)-(x1, y1), RGB(225, 0, 255)

'комбинация величин, выраженная в единицах энергии,
'получена для сравнения с другими величинами.
E = GN * M(0) ^ 2 / R(0)
Epshell = -p(0) * 4 * pi * R(0) ^ 3 * (5 / 3) 'условная потенциальная энергия оболочки
Ek = dEk(30000) 'кинетическая энергия всех частиц объекта
Ep = dEp(30000) 'потенциальная энергия всех частиц объекта
a = dA(30000) 'работа по сжатию объекта
RESULT4 = RESULT4 & " M(30000)/M(0)=" & M(30000) / M(0) & " E=" & E & " Epshell=" & Epshell & " Ek=" & Ek & " A=" & A & " Ep=" & Ep & " Virial=" & (Ep + Epshell) / (2 * (A + Ek)) & " T-dynamic=" & (2 / 3) * Ek / A
SavePicture Image, "radiation.bmp"

M(30000)/M(0)=6,25492722500597E-16
E=7,35953408325212E+26
Epshell=-1,20857483646375E+27
Ek=4,9279694414513E+26
A=3,28531296096751E+26
Ep=-4,34116723491992E+26
Virial=-1,00002135533046
T-dynamic=1,00000002980233

Результат T-dynamic=1,00000002980233 показывает, что законы термодинамики работают: U=3/2RT, A=RT, (2/3)Ek/A=(2/3)U/A.

Результат Virial=-1,00002135533046 показывает, что работает РАСШИРЕННАЯ теорема о вириале: Ep+Epshell=-2(A+Ek). См. Эффект Арки и теорема о вириале

Результат M(30000)/M(0)=6,25492722500597E-16 показывает, что масса исчерпана с точностью до 15 знаков, что соответствует возможностям ПК.

Программа для идеального газового объекта,
с учетом давления излучения.

К настоящему времени (02.12.2003) неясно, какая система уравнений точнее. Поэтому приводим две системы, но одну программу. Для того чтобы перейти на другую систему уравнений в программе необходимо переключить две строки: k, и p(i).

Несимметричная система уравнений.	Симметричная система уравнений
d(p+p')/dr = - g(mn+u'/c²) + 2(p-p₀)/r. dT/dr = - (2/3)mg/k. d(M+M')/dr = 4pr²(mn+u'/c²). g = G(M+M')/r². p=nkT. p' = (4/3)sT⁴/c.	d(p+p')/dr = - g(mn+u'/c²) + 2(p+p'-p₀)/r. dT/dr = - (2/3)mg/k. d(M+M')/dr = 4pr²(mn+u'/c²). g = G(M+M')/r². p=nkT. p' = (4/3)sT⁴/c.

В симметричной системе центр звезды представлен антивеществом. Но теряется теорема о вириале.
В несимметричной системе работает теорема о вириале. Точность сильно зависит о массы объекта, и размера программы. Здесь предлагается два варианта программы.

k = 33.8600892763602 'ДЛЯ АНТИСИММЕТРИЧНОГО УРАВНЕНИЯ
'k = 34.5359610028528 'ДЛЯ СИММЕТРИЧНОГО УРАВНЕНИЯ

lum = 3.846E+26 'мощность объекта (светимость)
msun = 1.9891E+30
Rsun = 696100000#
M(0) = 100 * msun 'масса объекта
R(0) = 300 * Rsun 'радиус объекта
dr = R(0) / 30000 'толщина слоя
g(0) = M(0) * GN / R(0) ^ 2 'ускорение g на поверхности объекта
T(0) = (lum / sigma / (4 * pi * R(0) ^ 2)) ^ (1 / 4) 'температура поверхности объекта
pr(0) = 4 * sigma * T(0) ^ 4 / c / 3 'давление оболочки / испущенного излучения
pm(0) = k * GN * M(0) ^ 2 * R(0) ^ (-11 / 2) * dr ^ (3 / 2) 'давление газа вещества, условная атмосфера
pshell = -(pr(0) + pm(0)) * 4 * pi * R(0) ^ 3 * (5 / 3) ' потенциальная энергия оболочки
n(0) = pm(0) / kB / T(0) ' концентрация частиц
dm(0) = n(0) * mat * 4 * pi * R(0) ^ 2 * dr 'условная масса нулевого слоя
For i = 1 To 29999
R(i) = R(i - 1) - dr
dm(i) = dm(i - 1) + 4 * pi * R(i) ^ 2 * (3 * pr(i - 1) / c ^ 2 + n(i - 1) * mat) * dr
M(i) = M(0) - dm(i)
g(i) = GN * M(i) / R(i) ^ 2
T(i) = T(i - 1) + mat * g(i) / kB * dr * (2 / 3)
pr(i) = 4 * sigma * T(i) ^ 4 / c / 3
'АНТИСИММЕТРИЧНОE УРАВНЕНИE
p(i) = p(i - 1) - (-mat * pm(i - 1) / kB / T(i) * g(i) - 3 * pr(i) / c ^ 2 * g(i) + 2 * (pm(i - 1) - pr(0)) / R(i)) * dr
'СИММЕТРИЧНОE УРАВНЕНИE
'p(i) = p(i - 1) - (-mat * pm(i - 1) / kB / T(i) * g(i) - 3 * pr(i) / c ^ 2 * g(i) + 2 * (pm(i - 1) + pr(i) - pr(0)) / R(i)) * dr
pm(i) = p(i) - pr(i)
n(i) = pm(i) / kB / T(i)
dEp(i) = dEp(i - 1) - GN * M(i) * (dm(i) - dm(i - 1)) / R(i)
dEk(i) = dEk(i - 1) + (3 / 2) * pm(i) * 4 * pi * R(i) ^ 2 * dr
dA(i) = dA(i - 1) + pm(i) * 4 * pi * R(i) ^ 2 * dr
dL(i) = dL(i - 1) + pr(i) * 12 * pi * R(i) ^ 2 * dr
Next

E = GN * M(0) ^ 2 / R(0) 'соотношение для сравнения с полученным ниже.
Ek = dEk(29995) 'кинетическая энергия всех частиц объекта
Ep = dEp(29995) 'потенциальная энергия всех частиц объекта
Еa = dA(29995) 'работа по сжатию объекта
El = dL(29995) 'энергия излучения внутри объекта

RESULT4 = RESULT4 & " pshell=" & pshell & " e=" & E & " EL=" & El & " Ek=" & Ek & " EA=" & ea & " Ep=" & Ep & " Virial=" & (-Ep - El) / (2 * (ea + Ek)) & " Tdynam=" & (3 / 2) * Еa / Eк

Выполнение программы с несимметричным уравнением дает: Virial=1,00733890096909 Tdynam=1,00000000000001.
Выполнение программы с симметричным уравнением дает: Virial=2,17483381036322 Tdynam=1,00000000000001.

С целью увеличить точность вычисления Virial, программа была чуть-чуть усложнена.
Вот пример для объекта с параметрами Солнца M = Msun, R = Rsun. Соответствует рисункам, показаным выше.

Dim k, Mob, Rob, M(30000), GN, h, c, sigma, mat, dr, pi, m0, mam(30000), dl(30000), dA(30000), dpr(30000), dpm(30000), dn(30000), dp(30000), dT(30000), pr(30000), pm(30000), dEk(30000), dEp(30000), a(30000), dM(30000), p(30000), n(30000), T(30000), R(30000), g(30000)
AutoRedraw = 1
'result1.Visible = True
'result2.Visible = True
result3.Visible = True
RESULT4.Visible = True
DrawWidth = 1
pi = 4 * Atn(1)
GN = 6.67259E-11 'Гравитационная константа
c = CDbl(299792458) 'скорость света
h = 6.62606876E-34
kB = 1.3806503E-23 ' постоянная Больцмана
sigma = 2 * pi ^ 5 * kB ^ 4 / (15 * h ^ 3 * c ^ 2)
mat = 2 * 1.66053873E-27 'масса частицы

k = 10.5691385995433 'коэффициент для несимметричной системы уравнений.
'k = 10.6459574294541 'коэффициент для симметричной системы уравнений.

dr = Rob / 30000
Rob = Rob + dr / 2
g(0) = Mob * GN / Rob ^ 2 'ускорение g на поверхности объекта
R(0) = Rob - dr 'радиус под нулевым ПОЛУслоем.
M(0) = g(0) * R(0) ^ 2 / GN 'масса под нулевым ПОЛУслоем.
dM(0) = Mob - M(0) 'разность масс.
T(0) = (3.846E+26 / sigma / (4 * pi * Rob ^ 2)) ^ (1 / 4) 't(0) = 5777
pr(0) = 4 * sigma * T(0) ^ 4 / c / 3
pm(0) = k * GN * Mob ^ 2 * Rob ^ (-15 / 2) * R(0) ^ 2 * (Rob - R(0)) ^ (3 / 2) 'эмпирическая формула для вычисления давления 30000-го слоя.
p(0) = pr(0) + pm(0)
n(0) = pm(0) / kB / T(0)
pshell = -p(0) * 4 * pi * Rob ^ 3 * (5 / 3)
dEp(0) = -GN * M(0) * dM(0) / R(0) 'потенциальная энергия нулевого слоя
dEk(0) = (3 / 2) * pm(0) * 4 * pi * R(0) ^ 2 * dr 'кинетическая энергия нулевого слоя
dA(0) = pm(0) * 4 * pi * R(0) ^ 2 * dr 'работа по сжатию нулевого слоя
dl(0) = pr(0) * 12 * pi * R(0) ^ 2 * dr
R(1) = R(0) - dr
dM(1) = dM(0) + 4 * pi * (R(1) + dr / 2) ^ 2 * n(0) * mat * dr
g(1) = GN * (M(0) - dM(1)) / R(1) ^ 2
T(1) = T(0) + mat * (g(1) + g(0)) / 2 / kB * dr * (2 / 3)
pr(1) = 4 * sigma * T(1) ^ 4 / c / 3
pm(1) = pm(0) - (-mat * pm(0) / kB / T(1) * g(1) + 2 * 2 * pm(0) / R(1)) * dr
p(1) = pr(1) + pm(1)
n(1) = pm(1) / kB / T(1)
dEp(1) = dEp(0) - GN * (Mob - dM(1)) * (dM(1) - dM(0)) / R(1)
dEk(1) = dEk(0) + (3 / 2) * pm(1) * 4 * pi * R(1) ^ 2 * dr
dA(1) = dA(0) + pm(1) * 4 * pi * R(1) ^ 2 * dr
dl(1) = dl(0) + pr(1) * 12 * pi * R(1) ^ 2 * dr
'вычисляем значения физических величин послойно и некоторые из них суммируем
For i = 2 To 29999
dpr(i) = pr(i - 1) - pr(i - 2)
dp(i) = p(i - 1) - p(i - 2)
dT(i) = T(i - 1) - T(i - 2)
dn(i) = n(i - 1) - n(i - 2)
dpm(i) = pm(i - 1) - pm(i - 2)
R(i) = R(i - 1) - dr
dM(i) = dM(i - 1) + 4 * pi * (R(i) + dr / 2) ^ 2 * (3 * (pr(i - 1) + dpr(i) / 2) / c ^ 2 + (n(i - 1) + dn(i) / 2) * mat) * dr
M(i) = Mob - dM(i)
g(i) = GN * M(i) / R(i) ^ 2
T(i) = T(i - 1) + mat * (g(i) + g(i - 1)) / 2 / kB * dr * (2 / 3)
pr(i) = 4 * sigma * T(i) ^ 4 / c / 3

'уравнение dp/dr для симметричной системы уравнений.
'p(i) = p(i - 1) - (-mat * (pm(i - 1) + dpm(i)) / kB / T(i) * g(i) - 3 * pr(i) / c ^ 2 * g(i) + 2 * (pm(i - 1) + dpm(i) + pr(i - 1) + dpr(i) - pr(0)) / (R(i))) * dr

'уравнение dp/dr для несимметричной системы уравнений.
p(i) = p(i - 1) - (-mat * (pm(i - 1) + dpm(i)) / kB / T(i) * g(i) - 3 * pr(i) / c ^ 2 * g(i) + 2 * (pm(i - 1) + dpm(i) - pr(0)) / (R(i))) * dr

pm(i) = p(i) - pr(i)
n(i) = pm(i) / kB / T(i)
dEp(i) = dEp(i - 1) - GN * M(i) * (dM(i) - dM(i - 1)) / (R(i) + dr / 2)
dEk(i) = dEk(i - 1) + (3 / 2) * pm(i) * 4 * pi * R(i) ^ 2 * dr
dA(i) = dA(i - 1) + pm(i) * 4 * pi * R(i) ^ 2 * dr
dl(i) = dl(i - 1) + pr(i) * 12 * pi * R(i) ^ 2 * dr

'вычисляем количество антивещества
If n(i) < 0 Then
mam(i) = mam(i - 1) - n(i) * 4 * pi * R(i) ^ 2 * mat
End If
Next

'Строим графики функций
For i = 2 To 29998
X = 1000 + i * (0.5) / 3
x1 = X + (0.5) / 3
'масса объекта под радиусом rr(i)
y = 6000 - M(i) / 6E+26
y1 = 6000 - M(i + 1) / 6E+26
Line (X, y)-(x1, y1), RGB(0, 200, 255)

'потенциальная энергия слоя
'y = 6000 - GN * M(i) * (dM(i) - dM(i - 1)) / R(i) / 1E+34
'y1 = 6000 - GN * M(i + 1) * (dM(i + 1) - dM(i)) / R(i + 1) / 1E+34
'Line (X, y)-(x1, y1), RGB(100, 200, 155)

'давление вещества в i-том слое
y = 6000 - pm(i - 1) / 13000000000#
y1 = 6000 - pm(i) / 13000000000#
Line (X, y)-(x1, y1), RGB(255, 0, 0)
'давление излучения в i-том слое
y = 6000 - pr(i - 1) / 13000000000#
y1 = 6000 - pr(i) / 13000000000#
Line (X, y)-(x1, y1), RGB(250, 250, 0)
'общее давление
y = 6000 - p(i - 1) / 13000000000#
y1 = 6000 - p(i) / 13000000000#
Line (X, y)-(x1, y1), RGB(250, 150, 0)
'концентрация в i-том слое
y = 6000 - n(i - 1) / 1.45E+26
y1 = 6000 - n(i) / 1.45E+26
Line (X, y)-(x1, y1), RGB(0, 255, 0)
'температура в i-том слое
y = 6000 - T(i) / 2700
y1 = 6000 - T(i + 1) / 2700
Line (X, y)-(x1, y1), RGB(220, 220, 220)
'ускорение g в i-том слое
y = 6000 - g(i) * 14.3
y1 = 6000 - g(i + 1) * 14.3
Line (X, y)-(x1, y1), RGB(225, 0, 255)
Next

E = (GN * Mob ^ 2 / Rob)
Ek = dEk(29999) 'кинетическая энергия всех частиц объекта
Ep = dEp(29999) 'потенциальная энергия всех частиц объекта
Ea = dA(29999) 'работа по сжатию объекта
EL = dl(29999)
Eam = mam(29999) * c ^ 2
RESULT4 = RESULT4 & " Eam=" & Eam & " e=" & E & " El=" & EL & " Ek=" & Ek & " Ea=" & Ea & " Ep=" & Ep & " Ratio=" & Ep / (Ea + Ek) / 2 & " ratio2=" & Ep / (EL / 2 + Ea + Ek) / 2 & " (2/3)Ek/A=" & (2 / 3) * Ek / Ea
SavePicture Image, "radiation.bmp"

Несимметричные уравнения дают: virial=0,999974429045177, Tdynam=1,00000002980233.
Симметричные уравнения дают: virial=1,00917324873147, Tdynam=1,00000002980233.

Это была страница, объясняющая принцип построения программы Модели Звезд, exe-файл, для решения системы дифференциальных уравнений, описывающих поведение физических величин в недрах гравитирующих объектов. Этот текст был написан в 2003 году. С тех пор программа была неоднократно усовершенствована, но сам принцип и главные выводы остались прежними.

Эффект Арки: Приложения. Куски программы.

Программа для идеального газового объекта без оболочки, записанная в Visual Basic.

Программа для идеального газового объекта, зажатого в оболочке

Программа для идеального газового объекта, с учетом давления излучения.

Программа для идеального газового объекта,
с учетом давления излучения.