Эффект Арки в тепловыделяющих средах. Поправка к уравнению гидростатического равновесия.

Можно ли проверить Эффект Арки на эксперименте?
Напрямую вряд ли.

Но есть еще одна возможность. Дело в том, что гравитационные процессы очень похожи на тепловые процессы.

Я утверждаю, что, если Эффект Арки реален, то:

Поместим в сферическую емкость радиоактивный газ.
Идет выделение тепла. Идет перенос импульса.

Графики для давления, концентрации, температуры будут подобны тем, что строит наша программа для газа, находящегося в гравитационном поле. То есть, в центре емкости давление будет таким же как и у оболочки. Максимум давления будет расположен на некотором расстоянии, которое определяем по нашим графикам.

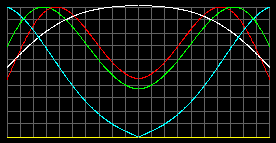
Зеленый - концентрация. Красный - давление вещества. Белый - температура. Фиолетовый - "ускорение", но уже не g=GM/r², как в гравитационном поле, а некоторая величина a.

Без учета Эффекта Арки максимум давления и концентрации будут в центре тепловыделяющей среды.

Чтобы нам не мешала конвекция, переместимся на ИСЗ. Но если тепловыделение сильное, то эффект будет заметен. Кроме того он будет проявлять себя и в жидком и в твердом теле.

Установите датчики давления в большой сферический кусок урана в реакторе, и я надеюсь, что вы увидите Эффект Арки

При переходе от слоя к слою, если dT/dr ≠ 0, мы замечаем, что скорость частиц меняется. Для каждого слоя среднеквадратичная скорость частицы газа определяется температурой слоя. Если мы проследим за воображаемой частицей, которая движется вдоль радиуса, не сталкивается с другими, и в каждом слое движется со скоростью, характерной для данного слоя, то мы получим ускоренное движение, и величину этого ускорения a. За пределами тепловыделяющей среды, но уже в однородной теплопроводящей среде ускорение будет спадать по закону обратных квадратов, как и для земного ускорения g.

Некто: Я полагаю многие могут сказать, как должно быть. Но что дает эксперимент - это уже знают единицы. Подобный эксперимент мало кому нужен. Кстати, какая разница давлений в максимуме и в центре по вашей теории? сколько %.

В принципе можно сделать 100%, можно 10000000%. . Чем выше разность температур между центром и оболочкой, тем выше разность давлений между оболочкой и точкой максимума. Если мы понизим температуру оболочки до нескольких К, а температура центра будет несколько тысяч К, то разность в давлениях у оболочки и в области максимума тоже будет исчисляться тысячами раз. Но у оболочки мы можем создать давление и 10, и 100 атм... Считайте, что будет в области максимума.

Кстати по зеленому графику, (т.е. по концентрации) можно определить угловое распределение вылетающих частиц, (нейтрино, нейтроны, гамма-кванты). Стандартная теория должна давать пик в центре, Арка дает минимум в центре.

Итог. Эффект Арки распространяется не только на гравитационные явления, но и на тепловые.

Так я предполагаю, что в тепловыделяющей среде работают те же уравнения, что и в гравитирующем теле. Получаемые графики должны быть подобными. А это значит, что для того чтобы узнать, чему равно давление в центре Солнца вовсе не обязательно отправлять туда датчики. Их достаточно расположить вдоль радиуса в тепловыделяющей среде, к примеру в урановом реакторе. Или в сфере, в которую помещен радиоактивный газ.

Если Эффект Арки реален то давление, концентрация и температура будут вести себя так, как показано на рисунке ниже.

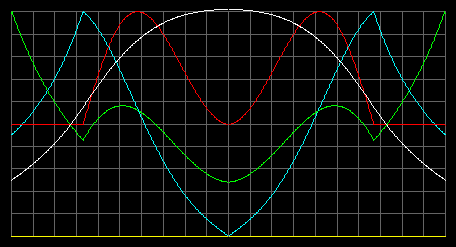
Зеленый - концентрация, красный - давление вещества, белый - температура, голубой - "ускорение".

Тепловыделяющий газ расположен в сфере радиусом 2/3 от радиуса. В пространстве между 2/3R и R находится теплопроводящий газ.

.	Гравитация.	Тепловыделение.	Гравитация и тепловыделение.
Градиент давления:	dp/dr=-rg+2(p-p₀)/r	dp/dr =-ra+2(p-p₀)/r	dp/dr =-r(g+a)+2(p-p₀)/r
Градиент температуры:	dT/dr = - (2/3)mg/k	dT/dr = -(2/5) ma/k	dT/dr = -(2/5) m(g+a)/k

В теплопроводящей среде в отличие от тепловыделяющей среды из уравнение dp/dr выпадет слагаемое -ra.

Если в объекте существует излучение, то формула в гравитирующе-тепловыделяющем объекте будет иметь вид:

d(p_вещ+p_свет)/dr =-(r_{вещ
+}r_свет)(g+a)+2(p_вещ-p₀)/r.

Величина a может иметь положительный и отрицательный знак. Если объект потребляет энергию космоса, то a отрицательна, если выделяет, то a положительна. В первом случае, в звезде преобладают эндотермические реакции. Во втором случае, в звезде преобладают экзотермические реакции.

Если газ состоит из нескольких компонентов, то в формулу будут входить столько же a_i, причем каждый из них может иметь свое значение, положительное или отрицательное. Это приводит к дифференциации вещества вдоль радиуса объекта. На поверхности мы будем наблюдать водород с мизерными добавками тяжелых элементов. Но программа показывает, что если у поверхности имеется хоть малая доля тяжелых элементов, то глубже объект представлен именно этими тяжелыми элементами.

Величина p₀ это давление оболочки, если таковая имеется. К примеру, давление резинового мячика, в который мы погрузили теплопроводящую среду, в центре которой имеется однородная тепловыделяющая среда. Кроме того, в p₀ могут вносить свой вклад силы поверхностного натяжения. Внутри газового объекта величина p₀ константа, "паскалево давление", но общее давление p переменно. Если объект твердый, то величина p₀ переменна и получает приращения за счет поперечных напряжений p_tв твердом теле. Радиальное напряжение p_r в этом случае играет роль переменного давления p, входящего в приведенные здесь формулы.

Если резиновой оболочки нет, то её роль может играть давление излучения p_свет. В этом случае при r=R, p_свет = p₀. Далее p_свет = p₀R²/r².

Это получаем из уравнения за пределами объекта dp_свет/dr =-2p_свет/r.

В современной термодинамике утверждается, что необратимые тепловые процессы порождают энтропию. Мы добавим, - необратимые гравитационные процессы поглощают энтропию.

Энергия Вселенной постоянна.
Энтропия Вселенной стремится к максимуму.

Эффект Арки объединяет гравитационно-тепловые процессы, и следовательно:

Энергия Вселенной постоянна.
Энтропия Вселенной постоянна.