Эффект Арки в моделях звезд, Солнца, идеального газового объекта в космосе.

А знаете ли вы, что Солнце можно считать полым газовым шаром?
К этому парадоксальному выводу я пришел в мае 2000 года. Я был потрясен результатами, к которым приводили вычисления и логика. Плотность и давление в звездах растут с ростом глубины лишь до определенного уровня. Это уровень, где тепловые скорости молекул становятся сравнимыми орбитальной скорости. При погружении ниже этого уровня плотность и давление газа должны падать. Многие звезды становятся почти пустыми внутри!

Этот вывод меня потряс. И не только меня. Я рассказал о нем своим детям, совершеннолетним парням, и они рассмеялись. А потом взял лист бумаги и показал логику...

Затем, через пару месяцев, я попытался запатентовать Гравитационно-Тепловую Катушку, работа которой, основана на том же принципе, что и в случае звезд, то есть, на новой форме уравнения гидростатического равновесия. Патентование длилось около года. Мне надоела бюрократия, и патентование я не довел до конца.

Но всякое "еретическое" решение нужно проверять разными способами. Падение плотности находило свое обоснование. А вот с падением давления мозг не хотел смиряться.

Два года меня давило сомнение.
Были моменты, когда я хотел даже внести поправки на страницы по Гравитационно-тепловой катушке, которые были размещены на моем web-сайте с 2000 года.

И только летом 2002 года, я нашел второй способ решения этой же задачи. Плотность и давление звезд действительно падают при погружении к центру, начиная с уровня, где тепловые скорости молекул сравнимы с орбитальной скоростью для этого уровня.

Данное решение полностью противоречит стандартным моделям звезд. Стандартные модели говорят, что плотность и давление в центрах звезд максимально. Но астрофизика недр звезд - это подтасовка, придуманная для того, чтобы объяснить источники звездной энергии реакциями термоядерного синтеза. Увы! "Термояд" не есть источник энергии Солнца и звезд.

В июле-августе 2002 года на Интернет-форуме "Альтернативная Наука" прошло обсуждение эффекта арки. (К сожалению, архивы пропали, и ссылки я удаляю 25.10.2003)

Я благодарю всех участников обсуждения, прежде всего Зубра, Давида М., Tiber, Vallav и др. Это обсуждение помогло мне утвердиться в своей правоте. В доказательстве ниже я применил несколько шагов, которые применял Tiber (Тиберкевич В.С.) в попытках опровергнуть Эффект Арки. Полученные ниже уравнения дают возможность оценить разные параметры в недрах Солнца и звезд. Благодаря тому же Tiber, выяснилось, что гравитепловая катушка не доказывает Эффект Арки. Арочное слагаемое, набегающее на одной половине витка Грави-Тепловой Катушки, сокращается набегающим арочным слагаемым на второй половине витка. Но ГТК все равно будет работать, но без учета Эффекта Арки. Далее идея ГТК переросла в отдельное направление: превратилась из стационарной Грави-Тепловой Катушки во вращающуюся Инерционно-Тепловую Катушку, которую я назвал Русская Тороидальная Матрешка. Она была предназначена для создания сверхвысоких давлений и осуществления в ней пресс-ядерных реакций синтеза. Как я ни старался улучшить её, но расчет показывал, что для начала реакций давление надо еще поднимать на пару порядков. И, наконец, выход был найден, - изменен тип реакции. Мной был найден третий уникальный элемент, который является сырьем для ядерной энергетики. D и U вы знаете. А о K узнаете попозже. Но это отдельная тема.

А здесь вернемся к Эффекту Арки, логическое доказательство которого, было получено в 2000-ом году. Ниже приводится доказательство, которое можно назвать аналитическим. Оно было получено в 2002 году. А в сентябре-октябре 2003-го года было получено новое, удивительно изящное доказательство, которое применимо не только к идеальному газу, но и к любому состоянию вещества. Его можно назвать математическим доказательством. Оно размещено на странице: Эффект Арки и уравнения равновесия. В 2003-ем году мной была создана, а в 2007-ом году доработана (darkenergy.narod.ru/arcru.exe) программа (exe-файл, 70 кб) для решения систем дифференциальных уравнений с учетом Эффекта Арки. Эта программа дала серию неожиданных результатов, анализ которых является еще одним, программным, доказательством существования Эффекта Арки. Есть и еще одно доказательство, - историческое. Оказывается, одним из первых, кто говорил о полых планетах и звездах был великий Леонард Эйлер. Именем Эйлера пропитаны основы физики и математики. Его имя встречается в учебниках и справочниках по физике и математике даже чаще, чем имя Эйнштейна. Следовательно, рейтинг мудрости Эйлера сравним, или даже выше рейтинга мудрости Эйнштейна. Эйлер либо первый, либо в числе первых. Его сложными уравнениями гидродинамики пользуются и сейчас. А простое уравнение гидростатики, применяемое сейчас, противоречит выводу Эйлера о полых планетах и звездах. Этот парадокс парадоксальней парадоксов СТО. Великие физики, не смогли понять этот вывод Эйлера. Поэтому они попадают в лагерь заблуждающегося большинства, а прав Эйлер. Следовательно, общепринятое уравнение гидростатического равновесия ошибочно. А новое уравнение, содержащее Эффект Арки, является более точным, т.к. соответствует выводам Эйлера.

Уравнение гидростатического равновесия, - стандартный подход.

Рассмотрим идеальный газ в гравитационном поле, силовые линии которого параллельны друг другу. Рассечем газ системой тонких слоев толщиной dr перпендикулярно силовым линиям. Давление передается от слоя к слою через силы упругости. Чем больше давление, тем ближе частицы находятся друг к другу. Если в некотором слое уже существует давление p, то давление в слое, лежащем ниже, будет p+dp. Где dp - давление, создаваемое верхним слоем. Для того чтобы его найти, нужно вес верхнего слоя, dP, разделить на его площадь:

Минус появился из-за того, что давление растет вниз, то есть, dp положительно при отрицательном dr. Представляя плотность через концентрацию частиц массой m, получим:

или через потенциальную энергию в гравитационном поле объекта:

Таким образом, мы получили классическое уравнение гидростатического равновесия, которое обычно применяется не только к полю с параллельными силовыми линиями, но и в сферически-симметричном случае, то есть, к планетам и звездам.

Дальнейший анализ показал, что в случае центральной симметрии классическое уравнение верно для идеального газа, состоящего из частиц не взаимодействующих между собой, но взаимодействующих с гравитационным полем всего объекта. Частицы такого идеального газа оказывают давление на стенки сосуда, в котором они находятся, но не давят на другие частицы газа. Примерами такого газа может быть очень разреженный газ с длиной свободного пробега сравнимого размеру объекта, звездные скопления, фотонный газ с температурой ниже миллиарда градусов...

Аналитическое доказательство Эффекта Арки.

Это доказательство, наверное, процентов на 80, принадлежит Tiber, который отстаивал общепринятую формулу, и изобретал для этого множество ходов, часть из которых мы здесь и используем.

Потенциальная и кинетическая энергии (U, E_кин) частицы газа, движущейся в гравитационном поле сферически-симметричного газового объекта постоянно изменяются на промежутке времени между двумя столкновениями с другими частицами, но сумма этих энергий остается постоянной. Поскольку выбор нуля для потенциальной энергии произволен, то мы можем положить, что сразу после столкновения с другой частицей её потенциальная энергия равна кинетической, но с обратным знаком. Тогда в любой момент времени до следующего столкновения сумма энергий U и E_кинбудет равна нулю.

Поскольку, между столкновениями частицы движутся по эллипсоподобным траекториям, то кинетическую энергию частицы можно расписать следующим образом:

где: u - радиальная скорость частицы; w - тангенциальная скорость частицы, E_u, E_w - соответственно радиальная и тангенциальная доли кинетической энергии. Ясно, что за радиальное приращение давления ответственна радиальная часть скорости частиц, или радиальная доля кинетической энергии. Подставим (3) в (2) и преобразуем полученное выражение.

Радиальная кинетическая энергия может быть заменена на эффективную потенциальную энергию, W, со знаком минус.

Изменение эффективной потенциальной энергии ответственно за изменение радиальной кинетической энергии. А изменение радиальной кинетической энергии ответственно за приращение радиального давления. Следовательно, вместо уравнения (1), верного для идеального газа в указанном выше смысле, мы можем записать уравнение для газового объекта, заменяя U на W, и снабжая некоторые величины дополнительным индексом _L. Индекс нам указывает на то, что данное приращение давление является парциальным, то есть, создается лишь n_L частицами, имеющими данный угловой момент L.

Формула (12) показывает, какое приращение давление создают n_L частиц, имеющих тангенциальную скорость w. Поскольку, давление есть величина аддитивная, то мы можем просуммировать все эти приращения:

dp/dr = - mg(n₁ + n₂ + … + n_i) + (m/r)*(n₁w₁ + n₂w₂ + … + n_iw_i)

Выражение (1/n) ₀∫^w.max w²dn есть среднее значение квадрата тангенциальной скорости [w²]. Следовательно, мы можем записать:

Если распределение скоростей изотропное, то

Учитывая связь между среднеквадратичной и наиболее вероятной скоростью, v_ср.кв.²=(3/2)v_вер², получим:

Используя выражения p=nkT, r=nm, (3/2)kT=mv_ср.кв.²/2, формула 17 можно заменить на формулу, не содержащую скорость частиц.

Таким образом, мы доказали, что уравнение гидростатического равновесия должно содержать арочное слагаемое 2p/r.

Применимость нового уравнения.

Компьютерный анализ нового уравнения гидростатического равновесия показал, что оно применимого к объектам различных масс, вплоть до масс больших планет. Если же мы переходим к звездам, то в это уравнение должно быть введено давление и масса излучения. Уравнение принимает вид:

Давление излучения не входит в последнее слагаемое этого уравнения. Причина такого поведения излучения понятна. Излучение не давит само на себя. Пересекающиеся лучи света не меняют своих направлений. Можно сказать, что свет обладает мнимым давлением, которое проявляется лишь в том случае, если в полость заполненную излучением внести экран из обычного вещества. Давление света есть лишь в том случае, если есть на что давить. Другими словами, излучение подчиняется классическому уравнению гидростатического равновесия, а вещество подчиняется новому уравнению. Если же имеется смесь из обычного газа и излучения, то верна формула (18).

Аналогичные рассуждения о мнимом давлении можно провести для скопления звезд. Звезды сами по себе в скоплении ведут себя, как частицы идеального газа. Но этот газ чрезвычайно разрежен. "Длина свободного пробега" звезд в звездном скоплении значительно больше радиуса скопления. Поэтому звезды не давят друг на друга. Давление появится только тогда, когда мы мысленно внесем большой и прочный экран внутрь звездного скопления. Поэтому, для звезд в звездном скоплении нужно пользоваться классическим уравнением гидростатического равновесия. Тогда мы получаем верную статистику распределения звезд в скоплении, а также классическую теорему о вириале. А в случае обычного газа теорема о вириале получает уточнение, - внутренняя энергия газа заменяется энтальпией.

А что если мы имеем газ, зажатый в полости? В этом случае нужно включить давление оболочки на газ, p₀.

Это уравнение можно использовать для звезд. Роль давления оболочки играет давление излучения, испускаемого звездой.

Если температура газа невысока, то p' и r' обнуляются:

Если самогравитация газа мала, к примеру, воздух в воздушном шарике, то слагаемое rg обнуляется. Давление p(r)становится равным p₀везде внутри воздушного шарика и тогда

Итоги.

Классическое уравнение гидростатического равновесия имеет очень ограниченную область применения: чрезвычайно разреженный газ, звезды в скоплениях, фотонный газ. Если же длина свободного пробега частицы газа значительно меньше радиуса объекта, то необходимо применять уравнение, содержащее арочное слагаемое. В астрофизике и геологии пользуются классическим уравнением, приводящим к максимуму давления и плотности в центрах массивных объектов. Использование наших уравнений приводит к минимумам давления и плотности в центрах массивных объектов, и даже к образованию газовых полостей в недрах планетах. Так внешнее ядро Земли, согласно классическим представлениям, жидкое. Но надежного обоснования этому нет. В нашем случае внешнее ядро Земли тоже жидкое, и этому есть обоснование. Переход в жидкую фазу начинается уже после прохождения максимума давления. То есть, вещество становится жидким там, где температура уже достигает 3-4 тысяч градусов, а давление уже прошло максимум и падает. Двигаясь дальше к центру Земли, замечаем, что на некоторой глубине жидкость переходит в плотный газ и далее давление газа падает почти до нуля в самом центре Земли. Область перехода жидкости в газ есть граница раздела между внешним и внутренним ядром планеты. В классической геологии предполагается, что внутреннее ядро Земли твердое. Кто прав - покажет время.

А пока, вот более реалистичная модель Земли.

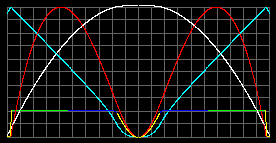Белый - температура; красный - давление; голубой - ускорение g;
разноцветный - концентрация частиц,
где: желтый - газ, зеленый - твердое вещество; синий - жидкость.

Объект, подобный Солнцу: M = 1M_Sun; R = 1R_Sun; m_particle= 1.5 а.е.м.

Наша модель	Стандартная модель

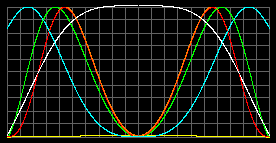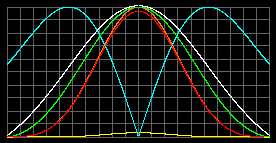T_center = 7.66 миллионов К. Общее максимальное давление p_max=8.4*10⁸атм при r=0.56R Плотность r_max=2.5 т/м³ при r=0.632R	T_max=18 миллионов К. p_max =7.96*10⁹атм в центре. r_max=7.8 т/м³ в центре.

Желтый - давление излучения; красный - давление вещества; оранжевый - общее давление.

Март, 2007. Обновлена программа darkenergy.narod.ru/arcru.exe Модели Звезд, exe-файл, txt-файл. Получены новые соотношения для теоремы о вириале. Добавлена конденсация газа в жидкость. Стало понятно, что стандартное уравнение гидростатического равновесия (dp/dr = -ρg) верно лишь для объектов с частицами с длиной свободного пробега больше радиуса объекта. А для обычного газа верно арочное уравнение: dp/dr = -ρg + 2p/r.

Весна, 2008. Создана программа darkenergy.narod.ru/arcbol.exe Аркбол-2008, exe-файл, моделирующая идеальный газ в собственном гравитационном поле. К сожалению, она не подтверждает ни арочное, ни общепринятое уравнение. Вероятная причина - частицы в программе имеют ненулевой радиус, а это уже неидеальный газ.