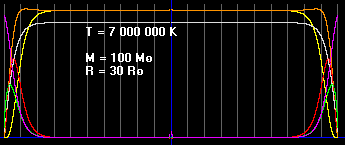Эффект Арки. Графики температуры, давления, плотности в недрах звезд, Солнца, планет, Земли.
Учет Эффекта Арки приводит к тому, что центры звезд, Солнца, больших планет и даже Земли, оказываются почти пустыми в центрах. Вот простейший пример для газового объекта.
| С учетом эффекта Арки. Альтернативная модель. |
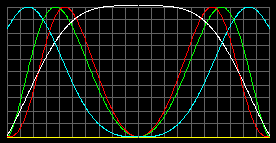
Без учета Эффекта Арки. Стандартная модель. |
 |
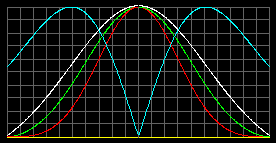 |
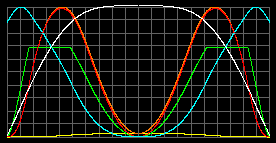
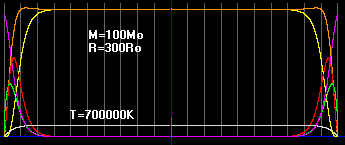
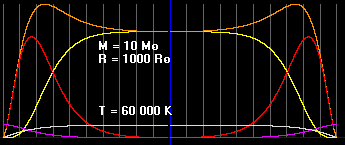
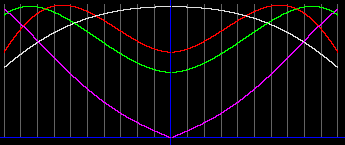
Красная линия отображает давление газа.
Зеленая - концентрацию частиц и плотность газа.
Белая - температуру газа.
Фиолетовая - ускорение свободного падения.
Графики построены на основании компьютерного решения систем дифференциальных уравнений.
| С учетом Эффекта Арки. Альтернативная модель. |
Без учета Эффекта Арки. Стандартная модель. |
| dp/dr = - gr
+ 2p/r. dT/dr = - (2/5)mg/k. dM/dr = 4pr2r. g = GM/r2. p=nkT. r=nm. |
dp/dr = - gr.
dT/dr = - (2/5)mg/k. dM/dr = 4pr2r. g = GM/r2. p=nkT. r=nm. |
Обозначения: p - давление; n - концентрация частиц; v - среднеквадратичная
скорость частиц; r - плотность; g - ускорение
свободного падения; M - масса объекта внутри радиуса r;
m - масса частицы; T - температура; G - гравитационная константа.
Попытки решить эту систему аналитически, оказались безуспешными. Но, имея под рукой компьютер, мы можем решить их графически, что и было сделано.
Газ, зажатый в оболочке.
Та же система уравнений, но в уравнение гидростатического равновесия входит слагаемое, содержащего давление оболочки на вещество p0.
dp/dr = - gr + 2(p-p0)/r.
Это уравнение может быть применимо к планетоподобным объектам. Роль растянутой оболочки, сдерживающей раскаленный газ, играет кора и верхние слои планеты, стягваемые силами Ван дер Ваальса, или силами поверхностного натяжения, но и теми, и другими, вероятно, можно далее пренебречь из-за малости. Роль давления оболочки может также играть излучение, испущенное звездой. Но и в этом случае оно поднимает графики почти незаметно. Для того чтобы графики поднялись на такую высоту, как показано на рисунке ниже, к "оболочке" нужно приложить температуру 9 млн. К., при том, что его масса и радиус равны Солнечным.
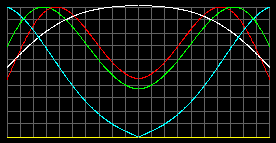
Графики давления, концентрации и температуры отрываются от нуля и выравниваются, по сравнению с графиками для свободного газа. Интересно то, что давление одинаково у границы емкости и в её центре.
Чем сильнее оболочка сжимает газ по сравнению с его собственным гравитационным стягиванием, тем ровнее графики. В предельном случае, когда силами само-гравитации газа можно пренебречь, значения давления, концентрации и температуры внутри емкости будут везде одинаковыми, что мы и наблюдаем в повседневной жизни. Примеры: воздушный шарик, капля воды и т.д.
Объект, подобный Солнцу: M = 1MСолн; R = 1RСолн; m = 1.5 а.е.м.
|
Наша модель |
Стандартная модель |
 |
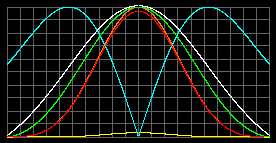 |
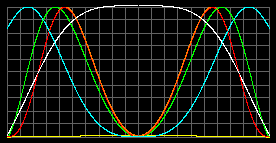
| Tцентр = 7.66 миллионов К. Общее максимальное давление pmax=8.4*108атм при r=0.56R Плотность rmax=2.5 т/м3 при r=0.632R |
Tцентр=18 миллионов К. pmax =7.96*109атм в центре. rmax=7.8 т/м3 в центре. |
Желтый - давление излучения; красный - давление вещества; оранжевый - общее давление.
Объект с массой M = 10MСолн; R = 50RСолн; m = 1.5 а.е.м.
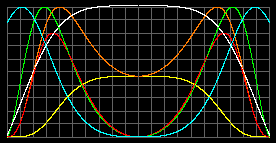 |
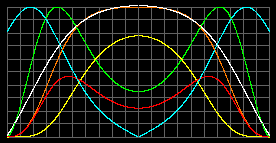 |
| Tцентр = 1.2 миллионов К.. pmax =1.2*104 атм при r=0,6R. rmax=0,19 кг/м3 при r=0,717R |
Tцентр=1.77 миллионов К. pmax =31519 атм в центре. rmax=0,2 кг/м3 при r=0,617R |
Давление излучения начинает оголять центр в обеих моделях. Давление и плотность недостаточны для осуществления термоядерного синтеза. В стандартной модели даже стараются не замечать давление излучения, чтобы синтез шел.
M = 70MСолн; R = 500RСолн; m = 1.5 а.е.м.
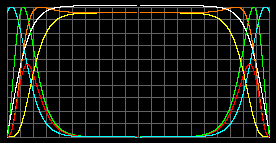 |
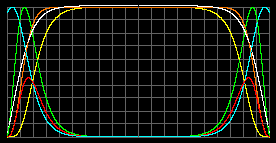 |
| Tцентр = 363 тысяч К. pmax =45 атм при r=0.74R. rmax=1.86 г/м3 при r=0.88R. |
Tцентр = 391 тысяч К. pmax = 58 атм в центре. rmax=1.81 г/м3 при r=0,87R. |
Воздушный шарик! И стандартную модель уже стандартной не назовешь.
Обратите внимание на значения полученных величин. Ядерные реакции в звездах
сверхгигантах невозможны. Но что произойдет, если мы уменьшим радиус в десять
раз.
M = 70MСолн; R = 50RСолн; m = 1.5 а.е.м.
Мы получаем почти такие же графики, но температура поднимется примерно в
10 раз, общее давление поднимется в 104 раз, потому что оно сейчас
зависит главным образом от излучения. Плотность увеличится в 103
раз. Но этого тоже недостаточно. Энергетические источники стандартной модели
исчезают.
Но не стоит брать близко к сердцу. Мы то знаем, что главный источник звездной энергии - поглощаемое пространство. И нам нужна более правдоподобная картина звездных недр. Давайте посмотрим на объекты с массой порядка солнечной, но с радиусом в сто раз меньше.
Белый карлик, M = 1MСолн; R = 0.01RСолн; m = 2 а.е.м. Плотность конденсации газа в жидкость (вырожденный газ) = 2*109 кг/м3.
|
|
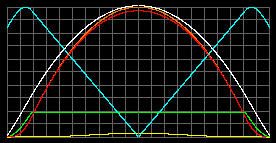 |
| Tцентр = 920 миллионов К. pmax = 6.9*1016 атм при r=0,581R. Жидкая фаза с rmax=2*109 кг/м3 простирается от 0.83R до 0.52R. |
Tцентр = 1249 миллионов К. pmax =2.1*1017атм в центре. Жидкая фаза с rmax=2*109 кг/м3 простирается от r=0,81R до центра. |
Ого! Обратите внимание на температуру. Не даром температура их поверхности превосходит Солнечную в несколько раз: 10000 K, 60000 K, и выше. (Разница в высоте графиков плотности является результатом программной нормировки. На самом деле была включена одинаковая плотность конденсации газа в жидкость, 2*109 кг/м3.)
Юпитер: M=0.00095MСолн; R = 0.1025RСолн;
m = 4 а.е.м. - взято произвольно.
С учетом того, что температура в области конденсации в стандартной модели значительно выше, чем в нашей модели, плотность конденсации возьмем равной 2000 кг/м3 для наших уравнений, и 6000 кг/м3 для стандартной модели.
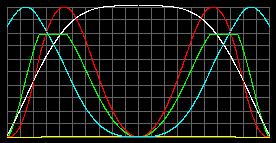 |
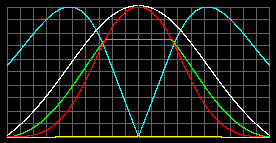 |
| Tцентр = 183 тысяч К. pmax = 6.4*106 атм при r=0.57R. Жидкая фаза с rmax=2000 кг/м3 простирается от 0.76R до 0.54R. |
Tцентр = 444 тысяч К. pmax = 6.4*107атм в центре. Жидкая фаза с rmax=6000 кг/м3 простирается от 0.25R до центра. |
Земля, масса частицы m = 20 а.е.м. - взято произвольно.
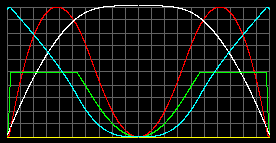 |
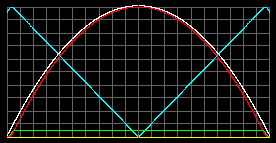 |
| Tцентр = 25 тысяч К. pmax = 6.6*105 атм при r=0.62R. Тверд/жидк фаза с rmax=6000 кг/м3 простирается от 0.97R до 0.47R. |
Tцентр = 33 тысяч К. pmax = 1.9*106 атм в центре. Тверд/жидк фаза с rmax=6000 кг/м3 простирается от 0.95R до центра. |
Разница в высоте графиков плотности является результатом программной нормировки. На самом деле была включена одинаковая плотность конденсации газа в жидкость, 6000 кг/м3.
Полученные значения температуры превосходят значения по данным сейсмологии примерно в пять раз. Температуру в центре мы можем понизить, уменьшив коэффициент в формуле для градиента температуры. Во всех случаях выше он был принят равным 2/5, что разумно для газообразной среды, но спорно для твердого/жидкого вещества. Понизим его произвольно до 1/10 и включим программу еще раз.
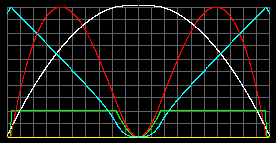 |
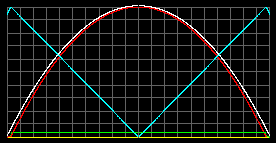 |
| Tцентр = 7.9 тысяч К. pmax = 7*105 атм при r=0.59R. Тверд/жидк фаза с rmax=6000 кг/м3 простирается от 0.97R до 0.17R. |
Tцентр = 8.2 тысяч К. pmax = 1.9*106 атм в центре. Тверд/жидк фаза с rmax=6000 кг/м3 простирается от 0.97R до центра. |
Давайте проанализируем графики в нашей модели. Падение давления начинается примерно при r=0.6R, но температура там уже достаточно высокая. Это значит, что где-то в этом районе должна существовать точка, где вещество начнет плавиться. Из сейсмологии известно, что граница между твердой мантией и жидким ядром расположена при r=0.54R. Эта граница сильно отражает P и S волны, и преломляет P-волны.
Наши графики давления и температуры показывают, что в нашем случае, действительно, горизонтальный график концентрации можно разделить на два участка: твердого и жидкого состояний вещества. В стандартной модели найти такую точку более проблематично, - давление растет до самого центра, а температура плавления пропорциональна давлению.
Наконец, давайте проанализируем точку перехода жидкости в газ. Это граница между внутренним и внешним ядром. Геология утверждает, что внутреннее ядро твердое, а внешнее ядро жидкое. Наши графики говорят о том, что внутреннее ядро газообразно.
Мы видим излом на графике концентрации частиц. Но из термодинамики известно, что при высоких температурах отличительной грани между жидкостью и газом нет. Поэтому, я вручную сглаживаю переход от внешнего ядра к внутреннему. Газовую фазу окрашиваю в желтый цвет, твердую - в зеленый, жидкую - в синий.
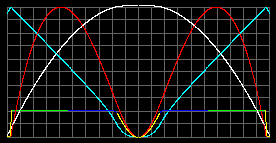 |
Внешнее ядро (синяя часть графика) пропускает лишь P-волны. Внутреннее ядро должно сдерживать любые сейсмические волны. Кстати, а как было открыто внутреннее ядро? Не по отражению ли от него P-волн.
Уравнения, использованные с учетом излучения.
| С учетом Эффекта Арки. Альтернативная модель. |
Без учета Эффекта Арки. Стандартная модель. |
| d(p+p')/dr = - g(r+r')+2p/r.
dT/dr = - (2/5)mg/k. dM/dr = 4pr2(r+r'). g = GM/r2. p=nkT. r=nm. r'=u/c2. u=3p'. u= 4sT4/c. |
d(p+p')/dr = - g(r+r'). dT/dr = - (2/5)mg/k. dM/dr = 4pr2(r+r'). g = GM/r2. p=nkT. r=nm. r'=u/c2. u=3p'. u= 4sT4/c. |
Когда мы включали возможность конденсации газа в жидкость, уравнение p=nkT или n=p/(kT) заменялось на:
| n = p/(kT) | если p/(kT) меньше чем nmax. |
| n = nmax. | если p/(kT) больше чем nmax. |
Уравнение температурного градиента.
Здесь мы испробовали два варианта для градиента температуры:
dT/dr = - (2/5)mg/k и dT/dr = - (1/10)mg/k.
В действительности это уравнение приближенное, - оно не содержит радиационной
части ('). Компьютерное моделирование показало, что включение радиационной
части существенно не повлияет на поведение графиков. С моей точки зрения,
коэффициент 2/5 применим для газа, с учетом Эффекта Арки,
а для идеального газа из невзаимодействующих частиц применим коэффициент
2/3. Поскольку такого газа нет, то пока забудем о
2/3.
Я бы назвал уравнение dTgrav/dr = - (2/5)mg/k уравнением гравитационного градиента температуры. Этот градиент не приводит к переносу теплоты, а возникает как гравитационный эффект. Перенос теплоты начнется в случае градиента dTtotal/dr = - ((2/5)+a)mg/k, где a - коэффициент температурного градиента, приводящего к теплопередаче. При расчете теплопередачи в радиальном направлении при наличии гравитационного поля следует брать уравнение dTthermal/dr = - amg/k
Компьютерное моделирование показало, что увеличение коэффициента ведет к смещению максимумов давления и плотности к границам объекта, а уменьшение - к центру. Поэтому реальные звезды, переносящие тепло из недр наружу, имеют общий коэффициент ((2/5)+a), больший чем (2/5), а значит, они еще больше похожи на воздушные шарики. С другой стороны, при очень высоких температурах и невысоких плотностях увеличится радиационный перенос энергии, что уменьшит и гравитационный, и общий градиент температуры. Если коэффициент слишком маленький, или равен нулю, (изотермический случай), то компьютер не может проинтегрировать систему, - все вещество сваливается к центру. Чтобы оно туда не свалилось, мы можем указать некоторое значение плотности, при котором газ больше не сжимается, а конденсируется в жидкость. Система уравнений снова становится интегрируемой.
Детальней о градиенте температуры смотри здесь: Гравитационный Градиент Температуры
Вы можете сами опробовать программу. Она загружена на "narod", exe-файл, 70 кб.
Текст выше написан в Марте 2007 г.
Текст ниже написан 13. 09. 2002: 02.12. 2003.
Исправления выделяю красным.
2007: Графики ниже построены с коэффициентом 2/3 в уравнении dT/dr. Думаю, что точнее так dT/dr = - (2/5)mg/k.
|
Красная линия - давление газа. Зеленая - плотность газа. Белая - температура. Фиолетовая - ускорение g. Даже для Земли графики будут подобны, но из-за сил Ван-дер-Ваальса, они слегка приподняты. 2007: Землю см. выше. |
Звезды малой массы и юпитеры |
| Появились еще два графика: желтый давление излучения, оранжевый общее давление вещества и излучения. Температура недр Солнца в полтора раза меньше, чем в стандартной модели. Если взять массовое число частиц меньше двух а.е.м., то температура недр в нашей модели будет еще ниже. |
Солнце |
| Вещество сконцентрировано в оболочке. Его давление значительно превосходит давление излучения лишь в интервале от 0.9R до R. Удивила сравнительно низкая температура, всего лишь 3 млн.К. В стандартной модели миллиарды К, но в той модели есть ядро, а в нашей модели - фотонная полость. |
Предсверхновая |
| Этот объект взрывается уже в компьютере. Внешние параметры подобрать очень сложно, - малейший сдвиг и центр разваливается. Тонкая оболочка, а внутри - огромный резервуар высокотемпературного излучения. |
Предельно неустойчивый голубой гигант, |
| И этот объект очень неустойчив, но его температура в десять раз меньше, а радиус в десять раз больше. Если оболочка состоит из прозрачного газа, или имеет высокую теплопроводность, то объект будет сжиматься. Графики очень похожие с графиками выше, но значения всех величин сильно отличаются. |
Сжимающийся красный или бордовый гигант |
| Вид графиков меняется только в случае изменения массы объекта. Графики этого объекта похожи на графики предсверхновой, но из-за большого радиуса, объект не взрывается, а напротив - сжимается. |
Сжимающаяся инфракрасная звезда-туманность |
| Из-за сил Ван-дер-Ваальса в коре объекта, состоящей из нейтронов, или вещества, кора и верхняя мантия играют роль резиновой оболочки воздушного шарика. Из-за этого графики поднимаются над нулем. Кора на графиках не изображена. В высокотемпературных карликах внутри появится излучение. Красная линия опустится вниз и появится желая. |
Нейтронная звезда, звезды карлики
и малые планеты. |
Фотонный газ, зажатый в полости.
Температура в центре звезды очень высокая, и исчисляется миллионами Кельвин. Центры звезд заполнены высокотемпературным излучением. Излучение имеет свое собственное давление, пропорциональное четвертой степени температуры. Следовательно, излучение выметает разреженное вещество из центра звезды.
Оказывается, что в фотонной полости звезды тоже работает эффект арки. На рисунке ниже показано, что давление, а также массовая плотность и удельная энергия излучения, имеют максимальное значение при r=exp(-1/2)*R. Однако этот максимум на графике давления не заметен (красная линия). Мы его получили путем построения графика p-p0, и увеличения масштаба по вертикали (зеленая линия).
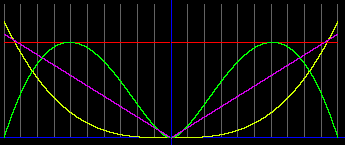
Желтой линией показана масса света, заключенного внутри радиуса r. Имеем в виду, что свет, замкнутый в полости, имеет массу, поскольку его суммарный импульс равен нулю. А свободный фотон массы не имеет, поскольку в этом случае он имеет импульс. Фиолетовой линией показано ускорение g. На графике мы видим прямую, но численный анализ показывает наличие кривизны. На первый взгляд может показаться, что это компьютерный артефакт. Однако, если мы задаем параметры фотонной полости, близкие к параметрам черной дыры, то кривизна графиков отчетливо видна. Это показано на следующем рисунке.
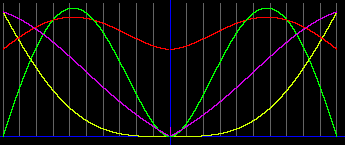
Для света, зажатого в полости, мы использовали уравнения:
dp'/dr = - gr' + 2(p'-p0)/r.
dM'/dr = 4pr2r'.
r' = 3p'/c2.
g = GM'/r2.
Некоторые величины мы снабдили штрихами, показывая, что эти величины относятся к излучению.
Смесь вещественного и фотонного газов.
Моделирование на компьютере показало, что вышеприведенные системы хорошо работают по отдельности, но их можно объединить лишь в следующем виде:
d(p+p')/dr = - g(r+r')+
2(p-p0)/r.
dT/dr = - (2/3)mg/k.
d(M+M')/dr = 4pr2(r+r').
g = G(M+M')/r2.
p=nkT.
p' = (4/3)sT4/c.
При этом оказалось, что M' пренебрежимо мала по сравнению с M. Это и понятно, - в нашей модели, из-за учета эффекта арки, температура недр предсверхновых упала с миллиардов градусов до миллионов. Грубо в 103 раз. Следовательно, массовая плотность излучения в недрах звезды падает в 1012, и M' можно из уравнений убрать.
Разочаровало то, что в уравнение для давления, излучение и вещество входят
не симметричным образом. Симметричное уравнение имело бы вид:
d(p+p')/dr = - g(r+r')+
2(p+p'-p0)/r,
но это уравнение при "графическом интегрировании", идя от поверхности звезды
к центру, порождает ядро из антивещества, что противоречит здравому смыслу.
Уравнение ведет себя нормально, если из последнего слагаемого убрать давление
излучения, p'. В чем же дело?
Причин может быть несколько:
1. Я чего-то не учел, или ошибся.
2. Дифференциальные уравнения для давления не аддитивны, в таком виде, как
я хотел их сложить.
3. Уравнения для излучения надо записывать с учетом релятивистской поправки,
которая может появиться перед g, или r.
4. 2007: При температурах порядка миллиарда градусов
фотоны проявляют корпускулярную природу, сталкиваются. Иногда порождают
электрон-позитронные пары. При этих температурах для света применим Эффект
Арки. При понижении температуры, длина свободного пробега фотона становится
сравнимой или больше радиуса объекта, и к ним Эффект Арки неприменим.
Проработаем третью версию. Запишем наше уравнение гидростатического равновесия для света:
dp'/dr = - gr' + 2(p'-p0)/r.
Учитывая, что в классической механике: g=v2/r, r'=u'/c2=3p'/c2, получим:
dp'/dr = 2p'/r * (1-(3/2)(v2/c2)) - 2p0/r.
Предположим, что для света коэффициент (1-(3/2)(v2/c2)) должен быть заменен на (1-(v2/c2)). Тогда:
dp'/dr = - (2/3) g u'/c2 + 2(p'-p0)/r.
Для того, чтобы это уравнение приобрело вид dp'/dr = - gr' + 2(p'-p0)/r, необходимо предположить, что коэффициент (2/3) входит либо в g'=(2/3)g, либо в r'=(2/3)u'/c2.
Л.Б.Окунь в статье "Понятие Массы", УФН, 158/3, 1989, стр.518, пишет:
"Однако при v/c~1 или v/c=1 мы сталкиваемся с принципиально новым явлением:
величина, играющая роль "гравитационной массы" релятивистской частицы, оказывается
зависящей не только от энергии частицы, но и от взаимного направления векторов
r и v. Если v || r, то "гравитационная масса" равна E/c2, но
если v^c, то она становится равной (E/c2)(1+b2),
а для фотона 2E/c2".
Если воспользоваться этой подсказкой Л.Б.Окуня, то массовая плотность света, r', уже должна содержать в себе коэффициент, но не (2/3) как нам хотелось бы, а (5/3).
Поэтому пока окончательных выводов делать не будем, а изучим этот вопрос более детально.
Гипотеза начала 80-х
В начале 80-ых годов, когда я учился в институте, нас здорово нагружали занятиями и подготовкой во внеурочное время. Тогда я уже был женат, и нам хотелось кое-где увильнуть, чтобы больше потратить времени на увеселительные мероприятия. Приходилось как-то приспосабливаться к большим нагрузкам. И мы специализировались: я решал жене задачи по физике и математике, а жена мне писала конспекты по политэкономии, философии, истории КПСС, и прочему атеизму. Как-то нам дали задание написать курсовые по физике. Тему мы могли выбрать сами. Я написал себе курсовую "Принцип неопределенности и проблемы астрофизики". А жене написал работу о недрах звезд. Названия работы я уже не помню. Но главная идея, заложенная в работу, - это гипотеза о звездах с ядром из антивещества. Как-то мне тогда удалось обосновать, почему ядро звезды и её периферия не вступают в аннигиляцию. Но вот прошло уже более двадцати лет, а это ядро из антивещества сейчас вылезло у меня на компьютере, и я никак не могу его изничтожить. Оно ведь портит красивые уравнения. Ядро из антивещества появляется, если мы используем уравнение гидростатического равновесия, симметричное относительно излучения и вещества: d(p+p')/dr = - g(r+r')+ 2(p+p'-p0)/r.
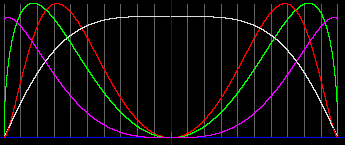
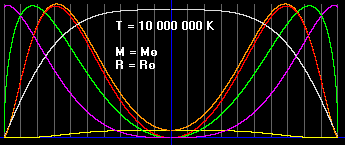
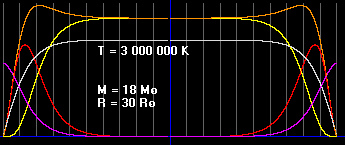
Ниже показаны графики для объекта с параметрами Солнца, и ещё ниже - для объекта с параметрами M=18MSun, R=30RSun.
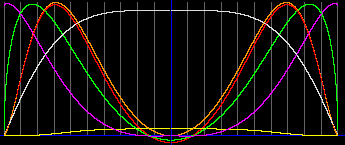
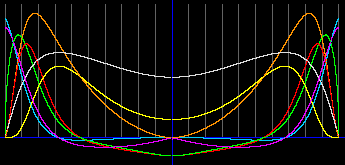
Конечно, это решение можно было бы выкинуть в помойку, тем более, что если оно и верно, то его всё равно не воспримет научная общественность. Жена тогда получила тройку за курсовую, а я - нагоняй от жены. Но на всякий случай, я оставляю графики. Здесь мне тройку уже никто не поставит.
Итак, если симметричное уравнение верно, то в объекте с параметрами Солнца, существует ядро из антивещества. Его радиус около 0.13RSun. В объекте массой M=18MSun ядро из антивещества имеет значительно больший радиус, 0.55RSun. Давление и концентрации вещества и антивещества на границе раздела равно рулю. Хотя давление излучения в этой области очень высокое.
Вывод
Новое уравнение гидростатического равновесия, полученного с учетом Эффекта Арки, хорошо описывает звезды и большие планеты. Мы получаем достаточно точные параметры в недрах объекта, если знаем его внешние параметры. Это уравнение неприменимо к объектам слишком большой массы, поскольку уравнение несимметричное, относительно излучения и вещества. Мы не знаем, какую релятивистскую поправку нужно использовать для таких объектов. (2007: Оно и должно быть несимметричным. При температурах до миллиарда градусов свет можно считать идеальным газом из не взаимодействующих между собой частиц.)
PS Вывод
Похоже, эта страница очень скоро будет опять изменена. Симметричные уравнения верны. А значит антиядра в звездах вполне реальны. (2007: Верны несимметричные уравнения.)
Другие страницы по Эффекту
Арки:
Эффект Арки в моделях звезд, Солнца, идеального
газового объекта в космосе.
Эффект Арки и теорема о вириале
Эффект Арки и уравнения равновесия
Тоннель Времени (Фантастическое развитие идеи).
Гравитационный градиент температуры.
Эффект Арки в тепловыделяющих средах.
Гравитационное зеркало. Фантастическое
развитие идеи.
Ядро Земли - раскаленная пустота.
Попытка поискать симметрии Ньютон/Кулон
Эффект Арки, приложения
К оглавлению Космической Генетики.
Страница создана: 13. 09. 2002.
Последнее обновление: 24.03. 2007.