Magnetic trap of Devil. Calculation.
In this column you will find two approaches to find the main characteristics of the magnetic trap. The first approach, named Nucleon Embedding, was invented in the autumn 2008 and was corrected in the beginning of 2009. The second approach, named Creation of Magnetic Hole, was received in March-April 2009. The results of both approaches coincided excellently. That means that the idea of magnetic trap is correct and the possibility of its creation on colliders is very high. That means that our Earth will be destroyed if we will not stop the powerful colliders. The third approach, named Characteristics of Magnetic Holes, leads to analogues results and splits on several possible branches.
The first approach. Nucleon Embedding.
Introductive amendment.
The creation of a magnetic hole is similar to composing of nuclei from nucleons.
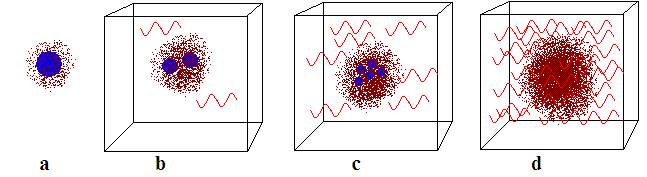
Let the mass of nucleon consists from two parts: the field mass of nucleon and the condensed mass of nucleon. Look at the fig. a: the field mass is depicted by the brown dots; the condensed mass - by blue circle. The field mass corresponds to the field of p-mesons, or to gluon field in more fresh interpretation. The condensed mass corresponds to the mass of naked nucleon or to the total mass of quarks in the nucleon.
The sum of masses of two free nucleons (proton and neutron) is bigger than the mass of deuteron, made from proton and neutron. The difference between the initial and final states corresponds to the binding energy of the created nuclei, deuteron. If we neglect the kinetic energies of particles in the initial and final states, then we can say, that the binding energy of nuclei is equal to the energy of emitted photons. In order to restore the equality of masses between initial and final states, we can put the interacting particles into a box with mirror walls. Thus we can add the mass of emitted radiation into the side of equation, corresponding to the final state.
At the process of further connecting of nucleons, we'll see, that the specific condensed mass of the resulting nuclei will be diminishing, and the field mass will be growing. The box will also be filled by more photons. Look at the fig. b and c, where blue circles becomes smaller, but the density of brown dots becomes bigger.

If there were only the nuclear forces inside the nuclei, then the moment will come, when the condensed mass would achieve the zero value. That is showed at the fig. d, where the radiuses of blue circles are already zero. But in the nuclei there are also the repulsive electric forces. These forces give no possibility to create the infinitely big nuclei. These forces are responsible for the iron peak in the periodical system of elements and for the existence of the final stabile element in periodical system. If there were no electric repulsive forces, then all nucleons would drop into the growing "nuclear hole", which would have no the limit of growth.
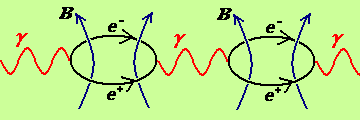
The growth of magnetic hole is similar to the growth of "nuclear hole". But here the proton, capturing by the hole, emits a positron; the neutron, dropping into the hole, emits an antineutrino.
Proton and neutron can be imagined as current pretzels with three poles:
u, u, d in proton
 ,
,
and d, d, u in neutron
 .
.
If the nucleon enters into a magnetic field, its current pretzel is undergo to the straightening forces. The more field - the more straightening forces - the more field mass - the less condensed mass. At last, when the field riches the critical value (1016 Tl), the nucleon undergo decay - its current pretzel with three mixed poles transforms into a vacuum current vortex, which is shown on the following figure in the form of a ring with two magnetic poles N and S.
The "memory about the proton's knot" is brought out by positron.
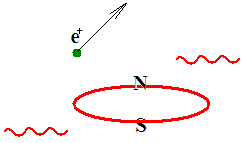
The "memory about the neutron's knot" is brought out by antineutrino.

In the above process the couple of photons are also emitted.
It is possible to compare the growth of the "nuclear hole" with the growth of the gravitational black hole.

The blue circles are masses, dropping to the event horizon, or moving around it on circumferences. If they are dropping, then their radiuses becomes less, and the density of brown dots will grow in the center of our figure. In this case the density of brown dots corresponds to the "power and depth" of a gravity funnel of eternally forming black hole. It is known that there are no completely formed black holes in the Universe. From the point of view of external observer, the object drops into the black hole infinitely long. So, it is possible to say that the mass of eternally forming black hole consists of two parts: the constantly diminishing mass of dropping objects (condensed mass, blue circles) and the mass of a black hole's funnel, or mass of BH's gravity field (field mass, brown dots). It is clear that at the time of a gravity collapse there will be the emission of photons, but I can not say now the fraction of it.
In the case of magnetic hole there are two eternally growing funnels, corresponding to N and S poles. The bottom calculation shows that at the time of magnetic collapse, the one thirds of rest energy of the captured matter goes into the growth of magnetic hole, and two thirds of captured energy are spent on radiation and on kinetic energy of emitted shell.
Calculation.
I have done a more detailed analysis of my old calculation and found
in it a mistake.
The minimum mass of a magnetic hole may be even less than it should have
from the first calculation.
But to define it precisely is not possible, because we do not know the magnetic
moment of a particle, which will remain after the capture of the nucleon
by magnetic hole.
Below I will talk about "imbedding".
Imbedding of nucleon into another nucleon, should not be taken literally.
This is an approximate calculation. Magnetic hole is not composed of nucleons.
It captures a neutron, and emits an antineutrino. It captures a proton,
and emits a positron. In both these cases it can spend its energy on the
kinetic energy of these ejected leptons and on radiation of photons. Magnetic
hole consists of bosons, quanta of magnetic field. The magnetic moment of
this boson is of course different from the magnetic moment of nucleon. Therefore,
our numerical result is an approximation.
Nucleon has a magnetic field. Consequently we can divide the energy of nucleon per two parts: the magnetic field energy and the energy connected with the restlet of nucleon, - condensed energy. The condensed energy is connected with its condensed-mass mR. The total condensed-mass of several connected particles depends from their quantity. Compare: the rest-mass of nucleus is also depend from the quantity of its nucleons, and this dependence in not linear.
At some critical number of captured nucleons, the hole's condensed-mass can be turned to be zero. In this case all its energy is concentrated in its magnetic field. That will be the minimal possible magnetic hole. It can be created at once, in the collision of two particle, but here we create it stage by stage, successively imbedding nucleons into it.
Let's neglect the rest mass of emitted positrons and neutrinos.
Let's imagine the nucleon as a ring contour with an electrical current,
creating the magnetic dipole moment, equal to experimental value of a nucleon's
dipole magnetic moment, p.
The energy of a ring contour is
E = pB.
It is concentrated in a magnetic field
B = μ0I / 2R.
Magnetic dipole moment is
p = IS.
After a simple transformation we can write the energy of magnetic field
E = μ0pRI2/2.
We supposed that the electric current was created by the movement of the elementary charge along the circular orbit of radius R with the speed of light. (The radius R is by p/pn times greater then the Compton radius of nucleon. Here pn is the nuclear magneton.)
Let's take a single nucleon. Its rest mass consists of two parts, - the mass of magnetic field and of the condensed mass of nucleon:
m = mmag.field + mR.
The energy of a nucleon is also consists of two parts:
mc2 = μ0pRI2/2 + mRc2.
Let's "imbed" two nucleons, one in one.
Neglect polarization and related changes in the dipole moment.
The energy of dinucleon's magnetic field will increase by 4 times because
of a the square over I2. In the right side of the equation,
we must add the energy of emitted photon, which is equal to pB=μ0pRI2/2.
It's origin: acceleration of one nucleon's magnet by another nucleon's magnet;
growth of kinetic energy and the loss of condensed mass; transition of kinetic
energy into the energy of the emitted radiation in the moment of nucleons
collision.
2mc2 = 22 μ0pRI2/2 + mRc2 + μ0pRI2/2.
Let's "imbed" the third nucleon. The energy of the thee-nucleon’s magnetic field will increase by 9 times. In the right side of the equation, we must add the energy of emitted photon, which is equal to p·2B. The energy of this photon is two times bigger than the energy of the first photon.
3mc2 = 32μ0pRI2/2 + mRc2 + μ0pRI2/2 + 2μ0pRI2/2.
Let's "imbed" the N-th nucleon. The energy of magnetic field of N-nucleon will increase by N2 times. In the right side of the equation, we must add the energy of emitted photon, which is equal to p (N-1) B. The resulting condensed mass, mR, becomes equal to zero.
Nmc2 = N2μ0pRI2/2 + μ0pRI2/2 + 2μ0pRI2/2 + ... + (N-1)μ0pRI2/2.
mc2 / (μ0pRI2/2) = (N2 + 1 + 2 + 3 + ... + (N-1)) / N.
Further absorption of nucleons can not lead to an increase in the magnetic
field, because the total condensed mass will be negative. Consequently,
we had received the value of critical magnetic field. The further capture
of nucleons by magnetic hole leads to the growth of the radius of a magnetic
hole.
The resulting value of the minimum possible energy of a magnetic hole corresponds
to the energy equal to one-third of TeV, which can be achieved even at Tevatron!
The right side in the last formula for large N is equal to (3/2)N.
Therefore, we can write
N = (2/3)mc2 / pB;
Bmax = NB.
2/3 of nucleon’s energy goes to the growth of the hole.
1/3 goes to radiation.
The last corresponds to the binding energy of the magnetic hole.
If we use the received formula N = (2/3)mc2 / pB for protons, we'll receive the total energy E, needed to create the minimal possible magnetic trap, and E will be equivalent to the rest energy of N protons. In this case N~510 and E~510mc2, or about 255mc2 per colliding proton.
If in the received formula N = (2/3)mc2 / pB for p we will use the magnetic moment of neutron then N~350.
The formula for N can be transformed to N=(4/3) (p/pn) / α, where α is the fine structure constant, 1/α = 137,036. If we suppose that the magnetic moment of resulting boson is equal to the nuclear magnetic moment, then the total energy, needed to create the minimal possible magnetic hole will be N = (4/3)/α = 183 a.u.m.
The results shows that the minimal possible magnetic hole can be made
at collisions with the energy about one-thirds of TeV per particle.
This energy is three times smaller than can be achieved at Tevatron!
-Why it was not been received yet?
Here are some possible explanations.
1. We do not know the magnetic moment of the resulting boson.
2. It is possible that magnetic hole could be born in a collision of two
quarks.
3. At the Tevatron they collide the protons with antiprotons and this lead
to the annihilation of the baryon number.
4. We do not know the magnetic polarization dependence.
5. It is not excluded that microscopic magnetic traps were already created,
and they are growing now somewhere inside the Earth.
The second approach. Creation of Magnetic Holes.es.
Let's find the value pB, where p is dipole magnetic moment of the first proton, and B is the magnetic induction, created inside the first proton by the second proton, flying beside the first proton. Let's solve the problem in the coordinate system, connected with the first proton. Magnetic induction is the variable value in time and in space.
B = μ0qvSin(v,r) / (4pr2).
Let's the second proton fly along the straight line, lying in the plane of the contour S of the first proton. The minimal possible distance rmin between the line and the border of the contour is defined by the equality of kinetic energy to the potential energy of two elementary charges Ekin = q2/(4pε0rmin).
The formula E = pB must by changed by the following one
dE = p (BdS) / S.
Let's create a computer program and the computer will compute and will sum up all dE, giving us in the result the total energy pB of magnetic field and its ratio to the rest energy.
At high energies the kinetic energy is the product of the particles momentum into the velocity of light, Ekin=Pc.
E2 = m2c4 + P2c2;
E2 = m2c4 + Ekin2;
Ekin = (E2 - m2c4)0.5.
The bottom figure corresponds to quite small energy of flying by proton, E ~ 1,3mc2.

The next figure: v=0,968c, E=4mc2.

The next figure: v=0,999999998c, E=160000mc2. In the coordinate system of collider: E*= 126mc2, or slightly more than 0,1 TeV.

The table of results for proton collisions.
The energy of flying proton: E = mc2/(α/2)2
= 75115,461mc2, or in the system of collider E* ~ mc2/(α/2)
= 2·137mc2,
| A \ B | 10 | 100 | 1000 | 10000 | 100000 |
| 1000 | 77,011 | 15,354 | 7,2235 | 6,8920 | 6,8895 |
| 10000 | 50,059 | 7,4219 | 1,8272 | 1,2671 | 1,2545 |
| 100000 | 37,304 | 5,1894 | 1,3317 | 0,9589 | Here |
| 1000000 | 31,027 | 4,6898 | 1,2868 | 0,9353 | is very |
| 10000000 | 29,481 | 4,6410 | 1,2830 | long | computation |
Column "A" means the number of computed and summed layers, nearest to the flying particle. The string "B" means the number of "rectangles" in one layer. It is visible that under B=10000 the precision of computation can be taken as quite good.
In the cells we can see the ratio (mc2) / (pB). The
conclusion can be made after the analyses of the results in the right bottom
corner of the table.
In the case the ratio more than 1, the magnetic trap for such energy is
impossible;
in the case the ratio is less than 1, the trap is possible;
in the case the ratio is equal to 1, the investigated energy is equal to
minimal energy needed to create the magnetic trap.
We can see that magnetic trap is possible for the upper case. In order to find the minimal energy, let's try the value Etotal = mc2(4/3)(p/pn)/α ~ 510mc2, which was received in the first approach for the total minimal energy, needed to create the magnetic trap. Dividing this energy by 2, we'll receive the energy of colliding proton in the collider, E ~ 255,2mc2. In the system of resting proton the flying proton must have the energy 65107mc2.
| A \ B | 10 | 100 | 1000 | 10000 | 100000 | 1000000 |
| 1000 | 77,013 | 15,359 | 7,2355 | 6,9043 | 6,90170 | 6,90167 |
| 10000 | 50,068 | 7,4397 | 1,8689 | 1,3292 | 1,31767 | 1,31755 |
| 100000 | 37,351 | 5,2482 | 1,3912 | 1,0269 | 1,0191 | |
| 1000000 | 31,237 | 4,7849 | 1,3486 | 1,0034 | ||
| 10000000 | 29,850 | 4,7418 | 1,3451 | ~ 1 | ||
| 100000000 | 29,808 | 4,7408 | ~ 1 |
Conclusion. The global catastrophe can be switched by magnetic trap, which can be made at proton collisions with 0.25TeV energy per proton.
Reproduction of biospheres and
civilizations. Who are you, dear reader:
"a cell of good reason", "a curiosity cell", or "thoughtless muscular cell"?
You are here:
Magnetic trap of Devil.
Recent calculations show that it is not excluded that microscopic
magnetic traps
were already created, and they are growing now somewhere inside the Earth.
Arguments, proving that "The
LHC will lead to global catastrophe"; "Magnetic holes exist";
"We will not be able to prevent the LHC launch and the following global
catastrophe". Religious and mystic arguments.
The failed report "What will LHC give us, the particle of God, or magnetic trap of Devil?"
The Letter to the President of Russia.
The Letters to the Prosecutors Office of the Russian Federation.
Let's make the Living Wall in front of LHC.
To index of Space Genetics
darkenergy@yandex.ru Ivan Gorelik
The third approach. Characteristics of Magnetic Holes.
This item was created in the period 16-25 April 2009.
Indexes 1, n, pr identifies the values
connected with the minimal magnetic hole; any magnetic hole, and proton,
correspondingly.
Suppose that the magnetic flux, penetrating the magnetic hole, is quantable.
Then, assuming that in the physical vacuum, there is a limiting magnetic
field and this field is a constant in the plane of the circle of magnetic
hole, then the radii and areas of the magnetic holes can form only a series
of specific values.
Let the minimum magnetic hole of radius R1, with the area S1 and the thickness d1, has the limiting magnetic field B1. The value B1S1 equals to one quantum of magnetic flux Φ1. Doubled quantum of magnetic flux is consistent with the values of R2, S2, d2, B2. At the bottom we will see that the limiting magnetic field does not depend on the radius, and that radius and thickness of the magnetic hole grow proportionally to each other.
At each point in the plane of the minimal magnetic hole there is a limiting current curl, created by the virtual electron-positron pairs. For the calculations, we can replace the limiting current curl into the equivalent current, created by elementary charges moving on a circle of radius R1 with the speed of light. The number of these imaginary elementary charges, is denoted by N1.
Then the expression for the current would take the form:
I1 = N1q / t = N1q
/ (2pR1 / c) = N1qc / 2pR1.
In = Nnqc / 2pRn.
Applying the known formulas Φ1 = B1S1; Φn = nh / 2q; B1 = μ0I1 / 2R1; c2 =1 / μ0ε0; q2 = 2αhcε0, we will find the number N.
N1 = 1 / α
~ 137,036.
Nn = n / α ~ n·137,036.
To prove the correctness of the formulas, send around a circle 137,036 elementary charges with the speed of light. Each of these charges creates a the center of the circle the magnetic induction B = μ0qc / 4pR2. Multiplying this expression by1/α and by the area of a circle, pR2, we'll get a quantum of magnetic flux, Φ1 = μ0qc / 4α = h / 2q.
Suppose that a proton, entering the magnetic field B, splits and his remaining boson condenses into a magnetic hole. Suppose that proton decay occurs when the energy of magnetic interaction between the hole's field B and a current in the proton Ipr, or with the magnetic moment of proton, will be equal to the rest energy of the proton, multiplied by some number x. We'll investigate here several options for different x-numbers, writing formulas one after another, painting them in different colors. Black color - a general formula for the quantum number n = 1, red - an interesting resonance; green - x transferred from right to left, to the nuclear magneton; blue - x is hidden in the proton magnetic anomaly, the black - a general formula for an arbitrary n.
B1IprSpr = xmc2.
B1IprSpr =2p2mc2.
B12pn
=mc2.
B1ppr =mc2.
BnIprSpr = xmc2.
Here: B1 = μ0I1 / 2R1 - magnetic induction of a minimal hole; I1 = qc / 2pαR1 - the current of imaginary charges of a hole; Ipr = qc / 2pRpr - the current of elementary charge in the proton; Spr = pRpr2 - Compton area of the proton; Rpr = h / 2pmprc - Compton radius of the proton. In the formula B12pn =mc2 the value 2pn is the supposed magnetic moment of the remained boson of decayed proton with a spin equal to 1, which explains the cause of "2-coefficient" appearance before the nuclear magneton pn. Formula B1ppr =mc2, containing the anomalous magnetic moment of the proton, ppr =2.7928pn, can be converted to a form B1IprSpr = xmc2, where x = 1/2.7928.
Applying the above formulas, we can get some characteristics of magnetic holes. The results will look more beautiful with the introduction of the replacement of y=(2x)0.5 and by using somewhere the proton's Compton length λpr = 2pRpr.
R1 = Rpr / y.
R1 = Rpr / 2p.
R1 = Rpr = 2,103089·10-16
m.
R1 = Rpr / 0,846
= 2,485228·10-16 m.
Rn = n0.5Rpr / y.
Current:
I1 = yqc / αλpr.
I1 = qc /
αRpr.
I1 = qc /
αλpr = 4981134 A.
I1 = 0,846qc /
αλpr. = 4215214 A.
In = yn0.5qc / αλpr.
Magnetic induction:
B1 = y2μ0qc
/ 4pαRpr2.
B1 = μ0pqc
/ αRpr2.
B1 =
μ0qc / 4pαRpr2
= 1,488162623·1016
Tl.
B1 = 0,8462μ0qc
/ 4pαRpr2
= 1,06569564·1016
Tl.
Bn = y2μ0qc
/ 4pαRpr2.
The first conclusion: Magnetic induction in the latter formula does not depend on n, hence, the magnetic induction is similar for the magnetic trap of any size. According to the above obtained dependencies Rn ~ n0.5 and In ~ n0.5, the current should grow proportionally to the radius.
The proper magnetic moment of elementary particles exceeds the orbital magnetic moment by two times. Suppose that the spin of remaining boson is equal to unity. Then the classical expression p = IS will receive the additional factor - "2".
p1 = 2I1S1 = Rprqc
/ yα
p1 = Rprqc / 2αp
p1 = Rprqc /
α = 1,384278304·10-24
J/Tl.
p1 = Rprqc /
0,846α
= 1,6358068·10-24
J/Tl.
pn = Rprn1.5qc / yα
The energy of a magnetic hole.
E1 = p1B1 = yhc
/ αλpr
E1 = p1B1 =
hc
/ αRpr
E1 = p1B1
= hc /
αλpr = 2,060031232·10-8
J, or 137.036mc2.
E1 = p1B1
= 0,846hc /
αλpr = 1,47521935·10-8
J.
En = pnBn = yhcn1.5 /
αλpr
Inductance of the minimal magnetic trap can be obtained by equating the energy LI2/2 and the energy E.
L1 = λpr
μ0 / y
L1 =
Rpr
μ0
L1 =
λpr
μ0 = 1,660532598·10-21
Гн.
L1 = λpr
μ0 /
0,846
= 1,962257543·10-21 Гн.
Ln = λprμ0n0.5
/ y.
Capacity of the magnetic trap can be obtained by equating the energy Q2 / 2C and the energy E. The charge Qn is defined by the above mentioned quantity of elementary charges q, Qn=nq/α.
C1 =
λprε0
/ y
.
C1 =
Rprε0.
C1 =
λprε0
= 1,17000110·10-26 F.
C1 = λprε0
/ 0,846
= 1,38259465·10-26
F.
Cn = λprε0n0.5
/ y.
The second conclusion: The astonishing simplicity of the formulas for inductance and capacity of the magnetic trap confirms its reality.
Threshold voltage is received, using the definition of capacity C = Q / U.
U1 = qy / αλprε0.
U1 =
q / αRprε0.
U1 =
q / αλprε0
= 1876544054 V.
U1 =
0,846q / αλprε0.
= 1343821425
V.
Un = n0.5yq / αλprε0
The period of the proper oscillations.
T1 =2p(L1C1)0.5
= 4p2Rpr/
yc.
T1 =2p(L1C1)0.5
= λpr
/ c. This period is equal to the proton's Compton
time.
T1 =2p(L1C1)0.5
= 4p2Rpr
/ c = 2,7694703·10-23
c.
T1 =2p(L1C1)0.5
= 4p2Rpr
/ 0,846c = 3,2726933·10-23
c.
Tn = 2p(LnCn)0.5
= 4n0.5p2Rpr
/ yc.
The wave resistance.
Z1 = U1 / I1 = Z0
Zn = Un / In = Z0
The value Z0 =(μ0/ε0)0.5 is the wave resistance of the physical vacuum. But the magnetic trap is not a wave, propagating in some direction with the speed of light. A stationary coordinate system can be associated with a magnetic hole.
Using the formula z = (R2 +(XL -XC)2)0.5 we can see that the total resistance of the magnetic trap is zero if its active resistance R is zero. It would indeed be zero, since the current in the circuit is created by a synchronous movement of the virtual particles.
Substituting our different L, C, T into the formulas XL= ωL= 2pL/T, XC = 1 / ωC = T / 2pC, z = (R2 +(XL -XC)2)0.5, we can make sure ourselves that they give the same results:
XL1= XL1
= XL1 = XL1
= XLn = μ0c
= (μ0/ε0)0.5
= Z0
XC1 = XC1 =
XC1 = XC1
= XCn= 1 / cε0
= (μ0/ε0)0.5
= Z0
z1 = z1 =
z1 = z1
= 0.
So, the hole has a magnetic inductance, capacity, their
own proper frequencies. Building on the analogy further, we can imagine
the magnetic hole in the form of a can, the lateral surface of which is
a one-loop coil and the lower and upper lids are the linings of the condenser.
Within a can, there are limiting current curls of virtual electron-positron
pairs, which we mentally moved on the side surface in the form of a current
of imaginary elementary charges.
Using the formulas for the capacity of flat capacitor, C =
ε0εS/d, and for
the inductance of one-loop (N=1) coil, L =
μ0μN2S/d,
and by comparing them with our formula Cn =
λprε0n0.5/y,
Ln = λprμ0n0.5/y,
Sn = pRn2,
Rn = n0.5Rpr/y, we can see, that the
thickness of the magnetic hole is exactly two times smaller than its radius.
dn = Rn / 2.
Conclusions.
So, what is a magnetic hole?
Given the results, obtained in this section, magnetic hole may represent one of the following four objects:
1. Permanent magnet, created by a current In
= yn0.5qc / αλpr
in the contour with the inductance Ln =
λprμ0n0.5
/ y;
2. Permanent magnet, created by a current I = In
in the contour with the inductance L = Ln/2
and simultaneously is an electric dipole, characterized by a constant voltage
U = Un , emerging between the lining of the condenser
with capacity C = Cn/2.
3. Oscillatory circuit, with alternating current, the amplitude value of
which is I~ = In, inside the inductance
L = Ln; and with variable voltage U~
= Un, emerging between the linings of the condenser with
capacity C = Cn.
4. The contour that creates a permanent magnetic field, provided by a constant
current Ic. The electromagnetic oscillations with the
amplitude value I~ can be created in the contour. The
values Ic and I~ can be arbitrary,
but Ic + I~ = In and
each of them is no more than In. L = Ln;
C = Cn.
In the second item, the calculated inductance and the capacity were divided by two, because it is logically correctly to assume that the energy of a magnetic hole E splits into two equal parts LI2/2 and CU2/2, not changing over the time. In the items 3 and 4, there is no dividing by two, because of fluctuations in those cases; because of simple energy transfer from the magnetic field into the electrical field and vice versa.
The most realistic items are the first and fourth option. The second option is possible if the virtual electrons and positrons in a constant magnetic field are removed from each other in the direction along of the strength lines of the magnetic field.
The energy of the magnetic hole grows proportionally to the cube of its radius. The period of oscillations increases proportionally to the radius. Frequency is the inverse value of the period. Estimated calculation shows that the magnetic hole, formed in the case of absorption of the Earth, will have a frequency about 1 MHz, with the absorption of the Sun - 10 kHz, with the absorption of the star of hundred solar masses - 1 kHz. Given the gravitational amendments, these frequency can be significantly increased by the gravitational redshift. This means that the observed frequencies of pulsars (up to 0.7 kHz) show that pulsars actually can be the magnetic holes, or containing holes in their centers, constraining the neutron shell from collapsing by its powerful magnetic field.
However, for objects with a mass of approximately one hundredth the mass of the Sun, the radiuses of the magnetic holes is less than the gravitational radiuses. But to judge the gravitational radiuses, we need to know, what is the gravitational mass of a magnetic hole? The fact that it has inertial mass, no doubt. But whether the gravitational mass and the inertial mass are equal in this case? And whether the gravitational field of a magnetic hole isotropic, or it has axial-symmetrical directivity pattern?
Estimated radius of a magnetic hole in the case of absorption
of the
Earth ~ 6 meters;
Sun ~ 400 meters;
Stars of 100 solar masses ~ 2 km.
We started from the quantized magnetic flux. In order to increase the magnetic flux per one unit, magnetic hole must absorb at the same time the packet of nucleons. The simultaneous absorption of "stack of nucleon" sounds sloppy. But for the first, why not absorb nucleons by stacks. Secondly, the quantization of magnetic flux can now be dropped - it was necessary only as a framework through which we performed the computations. And thirdly, it is not excluded that the magnetic hole can take any value of quantum number n, including fractional, but integers are resonant numbers, sought by the magnetic hole - such resonances, which planet seek in the solar system, are large lot.
What is Big Bang and who are bigbangers?
From discussion at forum.
Four-dimensional Rotation of the Universe.Four-dimensional Rotation you
can see here in the gif animated
picture.
If our Universe is closed, then it can rotate. The last observations
give several proves of this idea.
Somebody: Excellent 4-D information!
I've been re-working my "hypersphere" (4-D) theory of the Red Shift, but
things not going so well. Problem is that Hubble distance data actually
fits distance to stars even without "expanding" 4-D universe (so-called
"no center") but my theory does not seem to fit so well. I'm not even sure
why Hubble distance is a log function of red shift.
Thank you.
My H is the angular velocity of light in the hypersphere-universe.
It is H=73,3 km/s/Mpc or 2.37565(35)E-18 rot/s or 2.37565(35)E-18
rot/s.
This value gives us the CONVENTIONAL age of Universe: 13.3387(23) bln.years/rot.
Compare this value with CONVENTIONAL age of Earth: 365 days/rot.
The ACTUAL age of Universe is infinity.
If there is rotation then there is f=ma=mc2/R.
Every proton has quantum of action h - universal microrotation; and
quantum of force f, (h·ν0
= f·λ0) leading to universal
macrorotation.
Under the influence of this quantum of force every proton rotates in the
Universe, making the one full rotation per one Universal year, which is
equal to 13.34 bln.years.
The value ν0 is the
boundary frequency. ν0
= NH= 734.147!/s, (λ0=
408 km/!, t0=0.00136s/!)
This is the center of acoustic fluctuations.
This is the boundary between graviton and photon in 4-d quantum lattice
of Universe with the main quantum number N=3.09030·1020.
The sign ! is a "flash", the lattice parameter of macroscopic synchronization.
Our Universe is eternal and must have the eternal sources of energy.
The solution of Bell paradox gives the stellar sources of energy.
Macroscopic synchronization of matter in the gravity field leads to energy
output.
This source gives 2/3 of the solar energy output.
My formula of the stellar energy output (P~M4/R5)
coincides with observations and reminds the Hawking formula for BH evaporation
(P~M4/R6). Hawking formula leads to crisis under
subplankian values. The cause is clear.
Hawking did not used the main quantum number.
If we substitute the N in his formula we will go out from the crisis under
subplankian values, and we will receive the formula of stellar energy sources
in the ETERNAL Universe.
The second conclusion: if the corrected Hawking formula denies the black
holes, what star's explosions do we observe in the sky?
The answer is clear, - that is MAGNETIC holes.
Nucleon has the rest energy mc2.
It also has the magnetic energy, which is about 0.001 of it's rest energy.
If the nucleon will enter in the 1000 times stronger magnetic field, it's
magnetic energy will overpass its rest energy and the nucleon can decay.
Some theorists dream about the "monopole catalyses of proton's decay" at
the collider.
I say, that we will have no "monopole catalyses of proton's decay" but bose-condensation
of proton and neutron into magnetic trap of Devil. The condensation is accompanied
by emission of positrons and antineutrino from decaying protons and neutrons.
Resulting bosons will widen the surface of magnetic trap.
Magnetic trap has the constant critical field ~ 1016Tl.
The Earth can be transformed into magnetic trap with the radius about 6
meters.
Microscopic magnetic traps can be made on collider.
CERN scientists do not pay attention on my letters because they are slaves
of BB religion and want to test their religious theory at the collider.
BB - is a marasmatic theory.
BigBangers will make "Big Bang" from our Earth. But the Universe is eternal.