Alpha Method, CMB Temperature, Hubble Constant, Dark Energy.

Fine structure constant is one of the most wonderful physical constants, α = 1 / 137.036.. It characterizes the velocity of an electron in the hydrogen atom, and thus, it is the ratio between the two fundamental velocities in the microworld: c and αc. It splits some spectral lines in hydrogen atom such that ΔE = (α/4)²E_i. It sinks as a comb into the medium of other constants and divides them such, that the ratios between some of them are equal Alpha.

Let's take:
classical radius of an electron r_e=2.8179403E-15 m;
Compton wavelength of an electron, λ_e=2.42631021E-12 m.
Bohr radius of an electron, a_e=5.29177208E-11 m;
and Rydberg constant, Ryd=10973731.5685 m^-1.

In order to see α we must express these values in the similar form, for example, as wavelengths or length of circumference:

λ_class = 2π r_e = 1.77056410E-14 m;
λ_Compton = 2.42631021E-12 m;
λ_Bohr = 2π a_e= 3.32491846E-10 m;
(λ_Rydberg/2) = 1 / (2Ryd) = 4.55633525275E-08 m.

And now we can write:

λ_class / λ_Compton = λ_Compton / λ_Bohr = λ_Bohr / (λ_Rydberg/2) = α.

The question arises: where is the end of this row? It is not the simple question. We could receive the similar series, if we "nail" the electron in the hydrogen atom. Proton will be rotating around the nailed electron; will have another Bohr radius, but it's velocity will also be αc, if we demand the Bohr condition to be valid: mvr=nh/2π . For such proton we will be able to write down its Rydberg constant, its Compton wavelength, and its classical radius.

Let's go to big scales. According to the original version of Einstein's theory, the Universe was static and closed. He drew its model approximately thus:

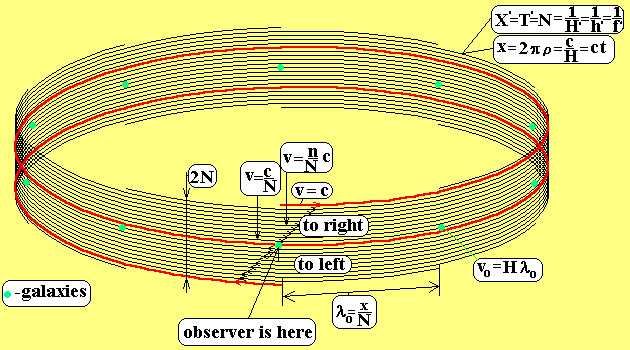
A tiny lamp was hung in the top point, inside the sphere. Its light went through the surface of the sphere and dropped the shades of the galaxies from the surface of the sphere onto the flat surface of the infinite table. The projection of the North Pole transforms from a point into a huge circumference, and it must be imagined in the infinite distance. That is why, under the transfer from the static model to the expanding model, it is logically correct to ascribe the value c to the receding velocity of the North Pole from the South Pole.

In this work we take exactly the same sphere, but we make the projection thus, that the radial scales would be unchanged. (Look the section Closed Universe, or the computer picture Universe, jpg 116 kb). All geometrical results will be the same, because the original sphere was the same. But now we have no the cause to ascribe the value c to the receding velocity of the N Pole.

On the contrary, if we want to build the discrete space-time, we will come to a conclusion, that the "receding velocity" of the N Pole, relatively S Pole must be equal c/2. Here is a picture the page Gravity.

The "residing velocity" is written here between the quotation marks because we build static model. In our static model a quantity of absorbed lines (energy levels) is equal to a quantity of newborn lines.

But if in our model the "velocity" between N and S is two times smaller, then the curvature radius in our model is two times smaller; volume is eight times smaller; density is eight times smaller than in the General Relativity.

ρ_GR = 3H²/(8π G), ρ = 3H²/(64π G).

If we use this equation for matter density, and if we equal the gravity force between two halves of the Universe to the force of radiation pressure on the surface, dividing the Universe on two halves, we'll receive the temperature of Cosmic Microwave Background Radiation:

F_gr=G(M_Un/2)² / R²; R = πρ_Un.

Curvature radius: ρ_Un= X/2π = c/2π H.

Gravity negative pressure: p_gravity = - F_gr/S; S = 4πρ_Un².

p_{radiation_non-Euclidean} = (π /4)*u_r = (π /4)*8π ⁵k⁴T⁴/(15c³h³).

p_{radiation_non-Euclidean} = - p_gravity

After some transformations we'll receive:

H = (2¹⁷π ⁹Gk⁴T⁴ /( 5*3³c⁵h³))^1/2 = 72.47 km/s/Mpc.

u_radiation / (ρ_matterc²) = 3/(2⁸π ³);
u_radiation / (ρ_electronc²) ~ 9π ²/2⁷.

From the other hand, if we use our value of Hubble constant, which was received earlier in this work (H =73.3 km/s/Mpc), we'll have:

T_our = 2.743 K; T_{CMB_observable} = 2.728+/-0.004 K.

The error in temperature: T_our / T_CMB = 1.0055;
or in pressure: p_gravity/p_{radiation_non-Euclidean} = 1.022.

Where is the error? What if our formula ρ = 3H²/(64π G) is also incorrect? Let's try very close formula:

ρ_α =2αH²/G.

If we take out α from this formula, we'll have:

α = ρ_αG/2H².

Now we use equations ρ_α = M/V; V = 2π ²ρ_Un³ = X³/(4π ) = c³/H³/(4π ) and we'll receive the ratio of radii:

α = (GM / c²) / ρ_Un.

The numerator is the radius of the orbital velocity, or the half of Schwarzschild radius for Universe's mass;
the denominator is the radius of the curvature of the Universe.

α = (ρ_Scharzschild/2) / ρ_Hubble.

Or thus:

λ_class / λ_Compton = λ_Compton / λ_Bohr = λ_Bohr / (λ_Rydberg/2) = .. = (λ_Scharzschild/2)/λ_Hubble=α.

If we perform the succession of steps as above, we'll have:

H = (8π ⁷Gk⁴T⁴ /( 15α²c⁵h³))^1/2 =74.09 km/s/Mpc.

(ρ_αc²) / u_radiation = 2π ²/α;
u_radiation / (ρ_electronc²) ~ 3π ³α.

From the other hand, if we use our value of Hubble constant, which was received earlier in this work (H =73.3 km/s/Mpc), we'll have:

T_α = 2.713 K; T_{CMB_observable} = 2.728+/-0.004 K.

The error in temperature: T_CMB / T_α = 1.0055;
or in pressure: p_{radiation_non-Euclidean} / p_gravity = 1.022.

If you compare these errors and the errors above you will see that Alpha splits the errors too! That was a joke, of course.

Alpha-method shows the correct way of further investigations. The formula ρ =2αH²/G describes the density of matter in the Universe. The density of electrons will be approximately 6π ⁵ times smaller. The density of radiation is comparable to the last. The radiation pressure must sustain the gravity of all these densities. May be, this will also solve the next riddle: "Why is the ratio of proton mass to electron mass so close to the number 6π ⁵?"

6π ⁵ = 1836.1181;
m_pr/m_el = 1836.1527.

It turned out to be, that the approximate equation m_pr/m_el ~ 6π ⁵ was received earlier, and it was explained in somewhat different ways:
Look, please, the web-page QUANTOLOGY of EL Hemetis, and the article ON THE MASS SPECTRUM OF NUCLEONS of Hans Hanson in Spec. Sci. Tech. ISSN 0155-7785, Vol 3, No 5, Dec. 1980.

Inserted the February, 15, 2003. In the beginning of this month the new excellent results were received. Look the section CMB = - Dark Energy.

According to this section the Alpha-cascade looks thus:
λ_class/λ_Compton=λ_Compton/λ_Bohr = λ_Bohr/(λ_Rydberg/2)=(8/3)(πλ_{Schwarzschild}/λ_Hubble)²=α.
(Note about the Tomson cross section: σ_T = (8/3)π r_class².)

And moreover, at extreme conditions, i.e., at energies of Grand Unification we have one more Alpha row:
α_GU = α_gravity = α_strong = α_weak = (8/3)α_el-magn.

According to this equation we have the new expression for the density of matter in the Universe:

ρ = ρ_critical * Ω

ρ_critical - critical density of the Universe;
Ω - relative density of the Universe, or, according to our conjecture, it is a gravity charge, which in it's turn, is equal to the square root from α_gravity or from (8/3)α_el-magn.

Thus we receive the formula for density of matter:
ρ = 3H² / (8piG) * ((8/3)α_el-magn)^1/2,
which can help us to compute the theoretical value of the temperature of CMB. Look this page: CMB = - Dark Energy

To the index of Space Genetics;

This page was made: the 8-th of February 2002.

darkenergy@yandex.ru

Ivan Gorelik

My VB-program SR2007.exe proves that the electron is not a point, but a string, embracing the whole Universe in a period, equal to electron's classic period.

Particles sew and stitch the space-time, constantly recharging electric and colour field, which are constituent subspaces of our whole macroscopic space-time.

Interested? Then go to the index of Space Genetics