4-D World

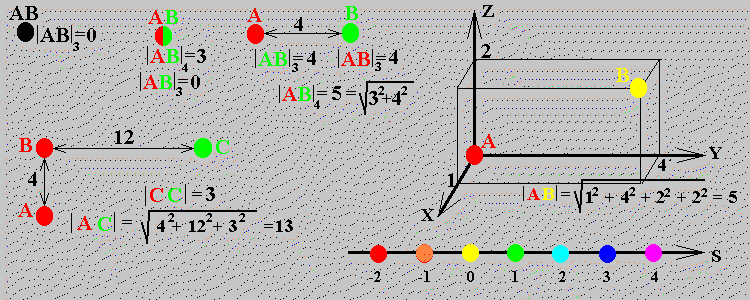
Zero-dimensional object is a point. One-dimensional infinite object is a line. One-dimensional finite object is a stretch. Two-dimensional objects are plane ones. Tree-dimensional infinite object is the space of our whole Universe, (if it would have the Euclidean geometry). Three-dimensional finite objects are a cube, ball, space of our room, and others. All these objects can be drawn on the two-dimensional leaf of paper. But what can we say about four-dimensional object? There is one method to draw it on two-dimensional paper: we must represent the fourth dimension with the help of colors. In the bottom picture you can see how to use colors.

At the up left corner we can see two coinciding points A and B. The three-dimensional distance between them is zero, |AB|₃=0. Slightly to right we can see these points, situated at the same coordinates x, y, z, but having different values on the fourth coordinate s. The point A is situated at s_A=-2; the point B is situated at s_B=1. The four-dimensional distance between these points is |AB|₄=3, but the three-dimensional distance is equal to zero, |AB|₃=0. After some training we can prove that the distance between two points in the 4d-space can be found from the equation: r²=x²+y²+z²+s².

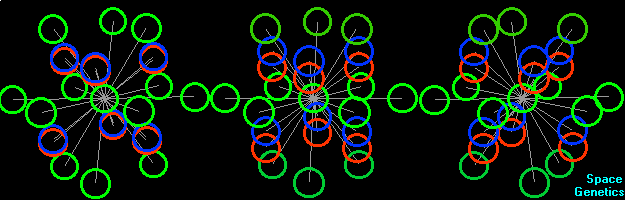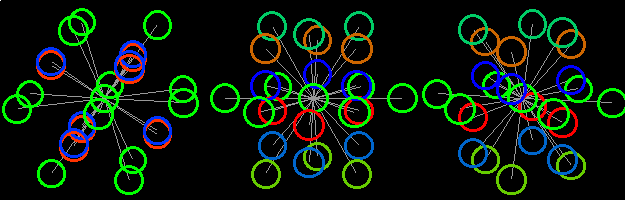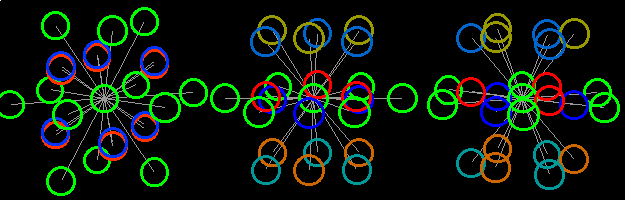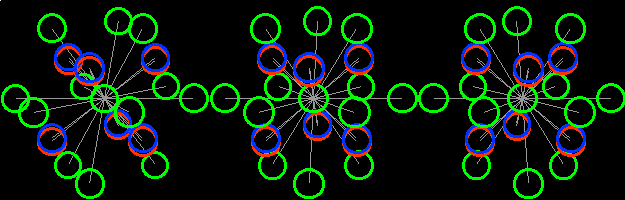
After some training you will also be able to understand the bottom picture. Look at the color scale of upper picture and say, what is the distance between players 6 and 7 on the bottom picture.

Look at the colors of the field’s boundaries and answer, please:

1. Are funs, denoted by numbers 1, inside the football field or outside it?
2. Does horse run on the football field?
3. Is the ball round?
4. What is the length of goals in the fourth dimension?

4D-box without two walls, perpendicular to color coordinate.

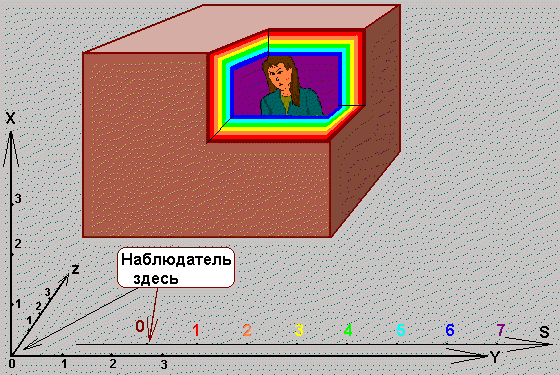
The woman, situated in that box, can leave it, if she will go to the infrared or ultraviolet side. In order this 4d-box was closed from all sides, one must imagine in that picture two additional 3-dimensional cubes: infrared and ultraviolet. These 3d-cubes will not hinder the woman, but she will not be able to leave such 4d-box, unless she would destroy one of eight walls.

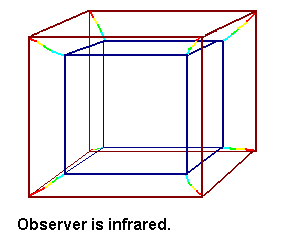
Wired frame, corresponding to 4d-cube. The observer looks at the box slightly from the right, upper, infrared side.

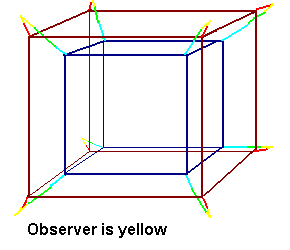
Wired frame, corresponding to 4d-cube. The observer looks at the box slightly from the right, upper side. Observer is yellow.

Several spheres of equal size, situated from the observer on equal distance on x, y, z, coordinates.
What is the color of observer?
Answer – brown, zero.

To understand this animated picture read the page 4D ROTATION AND SPHERE PACKING.

Our space-time is also 4d-space. But the time coordinate enters the space-time with the square root from "-1", which is usually denoted by the letter i. That is why our space-time is not Euclidean, but pseudo-Euclidean. On the bottom picture you can see the plane, build on the axes x and ict. The axis y can be imagined directed perpendicularly to the plane of this picture. The axis z can be imagined as color coordinate.

To understand this picture read the section Some Questions of SR.

At school we had learned what the Euclidean Geometry is.
Special Theory of Relativity gives us the notion about the pseudo-Euclidean Geometry.
But the space-time of our Universe is much more complex, and on the next stage we can try to understand what the non-Euclidean geometry is.

On the next picture you can see the example of non-Euclidean geometry. I draw this picture many years ago and asked my friends, - what is it? The answers were: Tardis, Bottle of Klein, Entrance to the Black Hole, Scale Changing Machine, UFO, Time-machine. What is it, if inside the first machine there is exactly the same second machine, inside the second machine there is the third machine, inside the third machine can be the fourth machine, and so on?

By the way, this picture is not so fictitious. There are some ideas of practical realization of this scale-changing machine. Moreover, the Universe can have distinctive features analogues to above shown geometry as a whole, and locally in some dust clouds. For more details about non-Euclidean geometry look the page Closed Universe and the computer picture Universe.

To index of Space Genetics

My Curriculum Vitae.

darkenergy@yandex.ru Ivan Gorelik.