
My Russian-language page is more informative.
Switch into Russian
In fact, in the most of cases we measure the velocity, which has no name in physics. Let's solve several simple problems.
Problem 1. You have made an ideal meter rod. Suppose it flew (sorry) in front of your nose in one second, sliding it slightly. What is the velocity of the rod?
If you divide one meter per one second, you will find an "error velocity". According to special relativity the moving rod is contracted.
d = d0sqr(1-v2/c2) = d0(1-v2/c2)(0.5).
According to the definition, the velocity is the ratio of the distance, covered by the material point, to the time interval of its movement. The length of the moving rod is smaller than one meter, consequently the trace, made by some point of rod on the coordinate plane will be smaller than one meter.
v = d0sqr(1-v2/c2) / t.
Velocity enters to both parts of this equation. After transformations we'll have:
v = b / sqr(1+b2/c2),
where: b = d0/t = 1m/s is "the error velocity", which we had received at the beginning. After computing we'll have:
v = 0,99999999999999999443674972... m/s.

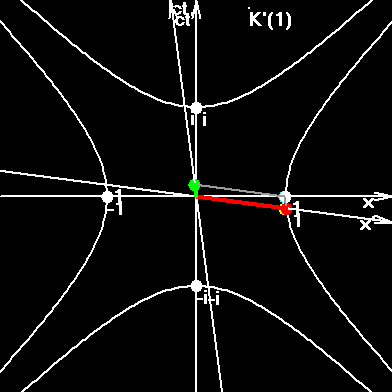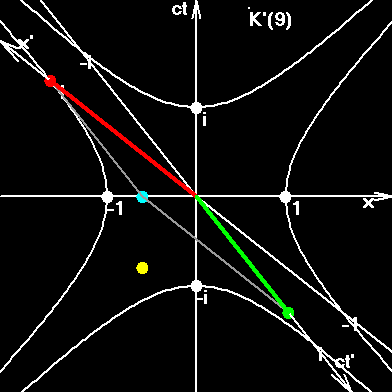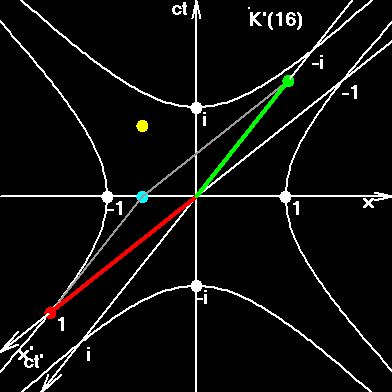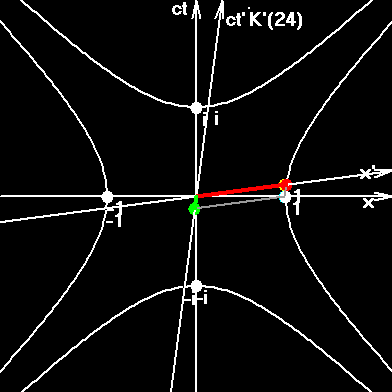
This figure shows how we can obtain two measurable values: "erroneous velocity" and "correct velocity". In order to measure the "erroneous velocity" you must tear out your nose and put instead of it a piece of chalk. Then you very gently slide a rod of known length against your chalky nose. You take the motion time from your wrist watch. In order to measure the "correct velocity" take a piece of chalk, attach it to the beginning of a moving rod (blue one of the figure), and let it slide against the resting rod (red one on the figure). In order to measure the motion time you must use two synchronized watches, placed at the start and finish points of chalk's trajectory.
Problem 2. You are in the uniformly moving car. At 12.00 you see the kilometer pole 100. At 13.00 you see the kilometer pole 200. What is the velocity of your car?
If you divide the covered distance 100 km by one hour you will receive "the error velocity" again. The role of moving rod in this problem plays the road. Road is contracted and the velocity will be a little smaller than 100 km/hour. If you don't believe me, open you car's door, bent your head to asphalt and touch it by your nose. Road slises by your nose. Road moves relatively you car’s reference system. Consequently the road is contracted... If you don't want to scribble your nose about asphalt - push out your hand out of the window, strike the kilometer poles by your hand, count the number of strikes. Divide this number per time of your movement, measured by your wrist watch and you'll have this damn “erroneous velocity”.
Problem 3. You are in the relativistic rocket with unlimited technical possibilities. Can you cover the distance of 1024 meters in a second?
If you rocket has unlimited technical possibilities then it is possible. Your "erroneous velocity" will be1024 meters per second, but the "correct velocity" will be smaller than 3*108 meters per second. In this problem the whole Universe plays the role of the upper contracted rod.
In fact, in our nature there are two types of measurable velocities. They are both real. Measurability must be comprehended here in the wider sense. The "erroneous velocity" is as much physical, as "the correct velocity" is. As we will see bottom "the correct velocity" is the hyperbolic tangent of rapidity, the "erroneous velocity" in the hyperbolic sine of rapidity. The coefficient of contraction is the hyperbolic cosine of rapidity. And the rapidity is the third type of velocity, but this value is not measurable. Let's analyze all these types of velocities, but at first let's introduce their definitions:
Coordinate time is the time measured by synchronized watches, placed everywhere in the coordinate system: t.
Coordinate velocity is the ratio of passed distance to the interval of time, measured by synchronized watches, placed at the start and finish points: v=dr/dt; v=vxi+vyj+vzk.
Proper time is the time, measured by the watch, connected with the moving object: t, dt=dt/g.
Proper velocity is the ratio of passed distance to the time measured by the watch, connected with the moving object: b=dr/dt; b=bxi+byj+bzk. Proper velocity is not limited by the value of speed of light. The limit of proper velocity is infinity. The proper velocity of light is infinity.
Speed is the absolute value of coordinate velocity. For example, speed of light is: c=299792458 m/s. v=|v|; v=sqr(vx2+vy2+vz2). In fact, the "ideal speedometer" does not measure the absolute value of coordinate velocity, but it measures the value of proper velocity.
Gamma is the coefficient of space contraction of the moving system, or time dilation in the moving system: g=1/sqr(1-v2/c2)=sqr(1+b2/c2).
Coordinate and proper velocities can be expressed symmetrically through each other
b = vg
= v/sqr(1-v2/c2);
v = b/g = b/sqr(1+b2/c2).
Velocities v and b are not additive ones. The law of velocities addition looks like hyperbolic tangent of the sum of two angles.
v = (v1+v2) / (1 + v1v2/c2),
v/c = (v1/c+v2/c) / (1 + (v1/c)(v2/c)),
thy = th(y1+y2)
= (thy1+thy2)
/ (1+thy1thy2).
That is why in the Special Relativity there were introduced two physical values: dimensionless parameter of rapidity y, and rapidity r with units of velocity.
y=y1+y2;
r=r1+r2;
r = y c.
Here are connections between v, b, g, y, r:
v/c = thy = th(r/c);
g = chy = ch(r/c);
b/c = shy = sh(r/c).
On the bottom figure one can see the graphs b/c=shy, v/c=thy, r/c=y.
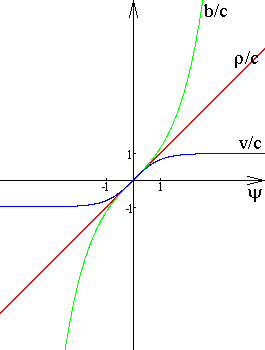
Here are some another comprehensible formulae:
y = r/c
= Arth(v/c) = (1/2)ln((1+v/c)/(1-v/c)),
y = r/c = Arsh(b/c)
= ln(b/c + g) = ln(b/c + sqr(1+b2/c2)),
y = r/c = Arch(sqr(1+b2/c2))=Arch(g).
The low of addition of several equal coordinate velocities:
v/c = thy = th(ny0) = th(nArth(v0/c)).
For several parallel vi, but not equal to each other:
v/c = th(Arth(v1/c)+Arth(v2/c)+Arth(v3/c)+...),
The low of addition of two proper velocities: b = b1g2+b2g1,
Compare: shy = sh(y1+y2)
= shy1chy2+shy2chy1.
The low of addition of several equal proper velocities:
b/c=shy=sh(ny0)=sh(nArsh(b0/c)).
For several parallel bi, but not equal to each other:
b/c=sh(Arsh(b1/c)+Arsh(b2/c)+Arsh(b3/c)+...).
Velocities can be also expressed though exponents:
v/c = thy = (ey-e-y)/(ey+e-y),
b/c = shy = (ey-e-y)/2,
g = chy = (ey+e-y)/2.
Let's try the formula g=sqr(1+b2/c2), using the known formula ch2y - sh2y = 1.
g2 - b2/c2 = (1+b2/c2) - b2/c2 = 1.
In the next sections we'll find the fourth, the most mysterious type of velocity, - the quantable velocity. Introduction of the quantable velocity explains why the electron is not a point particle, but it is a string, embracing the whole Universe at the the extremely short period of time, which is equal to the electrons classical period.
Model of Electron.
In order to understand this figure go ahead and read the next pages.
Forward to part 2: Interval. Four-dimensional velocities. Types of acceleration. Four-accelerations. Relativistic rocket.
Forward to part 3: Different forms of space-time transformations. Quantum velocities in Special Relativity. Model of electron.
Program of moving electron.
To index of Space Genetics.
darkenergy@yandex.ru Ivan Gorelik.