Разные формы записи преобразования координат в СТО.

Наиболее известными преобразованиями координат x и t являются преобразования, записанные через координатную скорость:

(1)
x' = (x - vt) / sqr(1 - v²/c²);
t' = (t - vx/c²) / sqr(1 - v²/c²).

Учитывая, что √(1 + b²/c²) = 1/√(1 - v²/c²) = γ, и b = vγ, получим преобразования, записанные через собственную скорость:

(2)
x' = xγ- bt;
t' = tγ - bx/c².

Учитывая, что γ = chΨ и b/c = shΨ, получим преобразования, записанные через параметр быстроты:

(3)
x' = x chΨ- ct shΨ ;
ct' = ct chΨ - x shΨ.

Запись через быстроту будет почти такой же, но вместо Ψпишем ρ/с.

(4)
x' = x ch(ρ/с) - ct sh(ρ/с);
ct' = ct ch(ρ/с) - x sh(ρ/с).

Перейдем от гиперболических функций вещественного аргумента к тригонометрическим функциям мнимого аргумента по формулам cos iΨ = ch Ψ; sin iΨ = i sh Ψ. Преобразования, которые мы получаем, связывают вещественную координату x и мнимую координату времени в псевдоевклидовом пространстве-времени:

(5)
x' = x cos iΨ+ ict sin iΨ ;
ict' = ict cos iΨ - x sin iΨ.

Эти преобразования в пространстве-времени почти ничем не отличаются от чисто пространственного поворота:

x' = x cos φ+ y sin φ ;
y' = y cos φ - x sin φ.

Отличие лишь в том, что чисто пространственный поворот осуществляется на вещественный угол φ, а пространственно-временной поворот описывается мнимым углом iΨ.

Несколько лет назад (2007) мне удалось найти еще одну скорость, квантованную. Сначала я её обозначил буквой q, потом v_q. А её параметр обозначил Q, причем Q=v_q/c. О ней поговорим на следующих страницах. А здесь укажем, на связь между координатной скоростью v, квантуемой скоростью q и ее параметром Q:
Q = q/c = arcsin(v/c), и запишем преобразования:

(6)
x' = (x - ct·sinQ)/cosQ;
ct' = (ct -x·sinQ)/cosQ.

Поворот в пространстве-времени.

Уравнение окружности в действительной плоскости имеет вид: x²+y²=r². Мы ясно понимаем, что этим уравнением задается множество точек, расположенных на расстоянии r от начала координат.

Перейдем в комплексную плоскость. Уравнение x²+y²=r² почти не меняется, за исключением того, что координата "y" становится мнимой, y=ib, а величина r² при этом может быть как положительным, так и отрицательным числом. А сам радиус будет либо положительным, либо чисто мнимым числом.

Итак, давайте нарисуем четыре гиперболы четырехмерного мира Минковского. Две из них, правая и левая, соответствуют псевдоокружности единичного радиуса. А верхняя и нижняя гиперболы соответствуют псевдоокружности радиуса i.

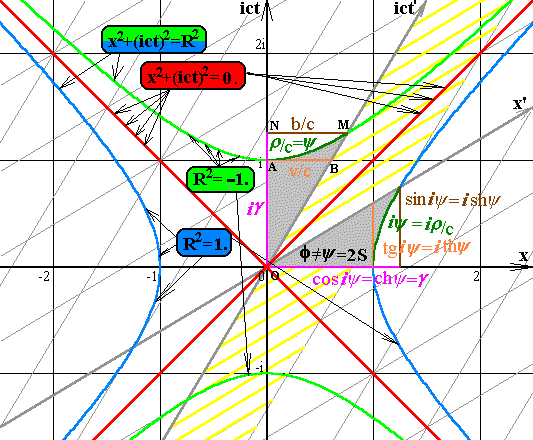
Простой подстановкой легко убедиться, что правая и левая гиперболы удовлетворяют уравнению x²+(ict)²=1. Верхняя и нижняя гиперболы удовлетворяют уравнению x²+(ict)²=-1. Квадрат радиуса псевдоокружности, окрашенной голубым цветом, равен единице. Квадрат радиуса зелёной псевдоокружности равен минус единице. А сам радиус является арифметическим корнем от квадрата радиуса, то есть для голубой псевдоокружности он равен единице, а для зеленой псевдоокружности он равен числу i. Визуально нам кажется, что расстояние от центра рисунка до разных точек псевдоокружности различно. Но имеем в виду, что это лишь удобный способ отображения псевдоевклидового пространства-времени на евклидову плоскость. Расстояния (интервалы) на этой плоскости вычисляются по формуле s=√((x₂-x₁)²+(ict₂-ict₁)²), а если вычисляем расстояние между центром и некоторой произвольной точкой, то s=√(x²+ict²)

Давайте выясним причину, почему при выполнении пространственно-временных преобразований ортогональные оси x и ict движутся либо навстречу друг другу, либо в разные стороны, но не в одну и ту же сторону.

Это связано с тем, что, если считать углом поворота отношение длины дуги к радиусу, то углы поворотов осей имеют разные знаки. Действительно, кусок дуги на правой гиперболе, окрашенный в темно-зеленый цвет, выражается мнимой величиной L_правый =iΨ, а радиус этой псевдоокружности равен единице. Пускай величина Ψ будет положительной, тогда ось OX будет поворачиваться против движения часовой стрелки, а поворот будет выражен формулой:

iΨ/ r = iΨ / 1 = iΨ.

Возьмём отношение длины дуги к радиусу в верхней гиперболе. Там длина дуги оказывается равной действительной величине Ψ, а радиус равен числу i. Тогда поворот будет равен отношению

Ψ / i = - iΨ.

То есть, угол поворота оси времени имеет противоположный знак, и эта ось движется навстречу оси OX. Этот поворот не следует воспринимать в привычном для нас смысле, поскольку он описывается мнимой величиной.

Другие замечания.

А. На первый взгляд, создается впечатление, что в преобразованиях (5)

x' = x cos iΨ+ ict sin iΨ;
ict' = ict cos iΨ - x sin iΨ,

одни слагаемые представлены действительными числами, а другие мнимыми. Однако это объясняется тем, что косинус мнимого угла в комплексной плоскости дает вещественное число, а синус дает мнимое число. Так в случае правой гиперболы косинус равен вещественному числу γ, поскольку является отношением вещественного прилежащего катета γ к вещественному радиусу, равному для правой гиперболы единице. В случае верхней гиперболы косинус есть отношение мнимого прилежащего катета iγ к мнимому радиусу i. Катет здесь оказывается больше гипотенузы, а косинус мнимого аргумента больше единицы. Синус мнимого угла iΨ=iρ/c в правой гиперболе есть отношение мнимого числа ib/c к вещественной единице, а в верхней гиперболе наоборот. Таким образом, преобразования работают и в такой форме записи. Подстановка значений косинуса и синуса в последние преобразования, возвращает преобразованиям вид в записи через собственную скорость

x' = xγ- bt;
t' = tγ - bx/c².

Б. Рисунок построен для скорости v=0,6c. Желтыми линиями показана мировая полоса движущегося стержня длиной один метр. Наклон линий соответствует линиям одновременности в движущейся системе.

В. Анализируя движение точки по гиперболе, замечаем, что отношение v/c всегда будет меньше единицы, в то время как b/c может принимать сколь угодно большие значения. Однако это не означает, что свет можно обогнать, т.к. собственная скорость самого света равна бесконечности. Параметр быстроты Ψгеометрически представляет собой комплексную длину дуги, измеренную в долях c, и показанную на рисунке темно-зеленым цветом. Численно величина Ψ может превосходить единицу, а ρ может превосходить с, но это не противоречит СТО.

Г. Длины темно-зеленых дуг на правой и верхней гиперболе равны друг другу с точностью до множителя i. Оказывается, что удвоенная площадь "сектора", окрашенного на рисунке темным цветом, дает это же число. Эту площадь можно вычислить в евклидовой плоскости, а длины дуг - в псевдоевклидовой. Поскольку в комплексной плоскости мы не можем измерить угол iΨ транспортиром непосредственно, мы можем записать выражения, заменяя величину Ψ на 2S. То есть, NM=sh(2S), ON=ch(2S), AB=th(2S). Кстати, ордината точки на обычной окружности единичного радиуса есть sin(2S), абсцисса есть cos(2S), ну и точка для tg(2S), расположена на касательной к окружности, подобно точке B, расположенной на касательной к гиперболе.

Д. Выше мы уже записали пять вариантов записи одних и тех же пространственно-временных преобразований. С учетом того, что между измеримым углом φ показанном на рисунке, и неизмеримой длиной дуги Ψ существует связь, tgφ= thΨ, мы можем без труда записать преобразования координат через угол, измеримый на рисунке. Для этого вернемся к преобразованиям (3)

x' = x chΨ- ct shΨ ;
ct' = ct chΨ - x shΨ.

Воспользовавшись формулами ch²Ψ=1/(1-th²Ψ) и sh²Ψ=th²Ψ/(1-th²Ψ), tgφ = thΨ, получим:

(7)
x' = (x - ct tgφ) / sqr(1-tg²φ);
ct' = (ct - x tgφ) / sqr(1-tg²φ).

Вперёд: Квантование скоростей в СТО.
Назад: Релятивистская ракета.
К оглавлению раздела Некоторые вопросы СТО.