Параметр быстроты Ψ, быстрота ρ.

Координатная и собственная скорости не являются аддитивными. Закон сложения сонаправленных координатных скоростей напоминают запись гиперболического тангенса от суммы двух углов. Это будет заметнее, если мы разделим обе стороны уравнения на с:

v = (v₁+v₂) / (1 + v₁v₂/c²),
v/c = (v₁/c+v₂/c) / (1 + (v₁/c)(v₂/c)),
thΨ = th(Ψ₁+Ψ₂) = (thΨ₁+thΨ₂) / (1+thΨ₁thΨ₂).

Угол, в отличие от тангенса угла, - величина аддитивная. Поэтому в специальной теории относительности были введены безразмерный параметр быстроты Ψ и быстрота ρ, размерность которой совпадает с размерностью скорости.

Ψ = Ψ₁ + Ψ₂;
ρ = ρ₁ + ρ₂;
ρ = Ψ c.

Координатная скорость и коэффициент гамма могут быть выражены через гиперболические функции от этих величин. Оказалось, что собственная скорость дополняет данную группу равенств

v/c = thΨ = th(ρ/c);
γ = chΨ = ch(ρ/c);
b/c = shΨ = sh(ρ/c).

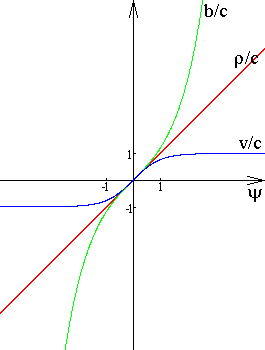
На рисунке ниже показаны графики b/c=shΨ, v/c=thΨ, ρ/c=Ψ.

Параметр быстроты и быстроту можно получить по формулам

Ψ= ρ/c = Arth(v/c) = (1/2)ln((1+v/c)/(1-v/c)),
Ψ = ρ/c = Arsh(b/c) = ln(b/c + γ) = ln(b/c + sqr(1+b²/c²)),
Ψ = ρ/c = Arch(sqr(1+b²/c²))=Arch(γ).

Закон сложения для множества одинаковых сонаправленных координатных скоростей v₀ может быть записан в виде

v/c = thΨ = th(nΨ₀) = th(nArth(v₀/c)).

Или для множества v_i, параллельных между собой, но разных по абсолютному значению:

v/c = th(Arth(v₁/c)+Arth(v₂/c)+Arth(v₃/c)+...),

Закон сложения сонаправленных собственных скоростей напоминает выражения для синуса гиперболического от суммы двух углов:

b = b₁γ₂+b₂γ₁,
shΨ = sh(Ψ₁+Ψ₂) = shΨ₁chΨ₂+shΨ₂chΨ₁.

Для множества одинаковых сонаправленных собственных скоростей b₀ получим:

b/c=shΨ=sh(nΨ₀)=sh(nArsh(b₀/c)).

Или для множества b_i, параллельных между собой, но разных по абсолютному значению:

b/c=sh(Arsh(b₁/c)+Arsh(b₂/c)+Arsh(b₃/c)+...).

Эти величины можно выразить через экспоненты:

v/c = thΨ = (e^Ψ-e^-Ψ)/(e^Ψ+e^-Ψ),

b/c = shΨ = (e^Ψ-e^-Ψ)/2,

γ = chΨ = (e^Ψ+e^-Ψ)/2.

Пользуясь соотношением ch²Ψ - sh²Ψ = 1, проверим справедливость формулы γ=√(1+b²/c²):

γ² - b²/c² = (1+b²/c²) - b²/c² = 1.

Примечание:

Если система K' (вагон) движется относительно системы K (вокзал) со скоростью v₁, и, если некоторая точка движется в системе K' со скоростью v₂, направленной под углом α к скорости, то скорость этой точки относительно системы K будет определяться по формуле:

v² = (v₁² + v₂² + 2v₁v₂Cosα - c^-2 v₁²v₂²Sin²α) / (1 + c^-2v₁v₂Cosα)². Einstein A Jahrbuch Radioaktivitat Elektronik 411 (1908) p. 423.

Результирующий мнимый угол поворота  φ = iΨ можно получить по формуле Зоммерфельда (1909):

cosφ = cosφ₁cosφ₂ - sinφ₁ sinφ₂cosα.

Пользуясь формулами cosφ = cos iΨ= ch Ψ; sin φ = sin iΨ = i shΨ, формула Зоммерфельда дает выражение для результирующего параметра быстроты:

chΨ= chΨ₁chΨ₂ + shΨ₁ shΨ₂cosα.

Используя связь между γ = ch Ψ = 1/cosQ, можно получить формулу для результирующего параметра квантуемой скорости, о которой мы поговорим в следующих разделах:

cosQ = cosQ₁cosQ₂ / (1+ sinQ₁ sinQ₂cosα).

И окончательно, для результирующего коэффициента γ и результирующей собственной скорости:

γ = γ₁γ₂ + b₁b₂cosα = γ₁γ₂(1 + v₁v₂cosα).

b² = (γ₁γ₂ + b₁b₂cosα)² - 1.

Дальше: Интервал.
Назад: Два вида измеримых скоростей в СТО.
К оглавлению раздела Некоторые вопросы СТО.