The electron is not a
point, but a string, embracing the whole Universe in a classic electron's period,
t = l/c = 9.4×10-24 seconds.
It flies around the Universe
106 400 000 000 000 000 000 000 times per second!
Is it possible?
Yes!
The cause is in the following. The most of it's time electron moves along the isotropic line. The length of isotropic line is zero.

Model of electron.
I'll write now very simplified model. More detailed explanations and proofs will be added further.
Let the center of this figure be the electron's center. At any given moment of time it can be empty. But if we take sufficiently long period of time, then the mentioned centers coincide.
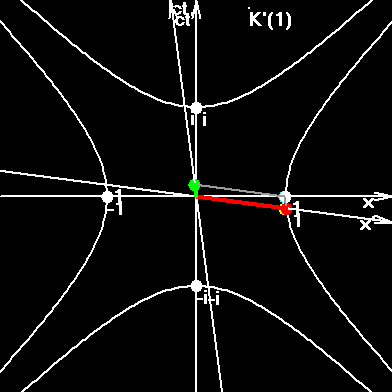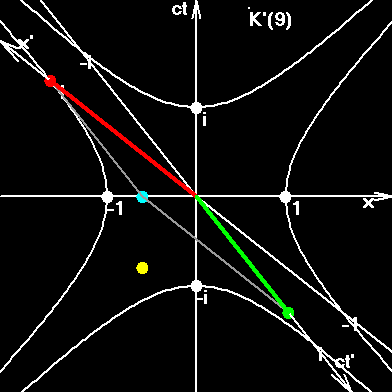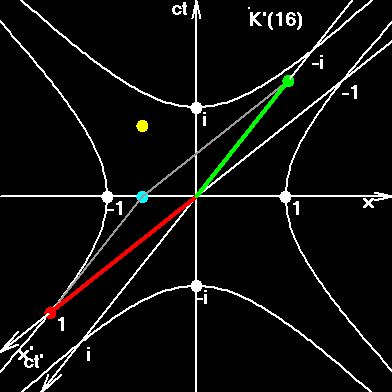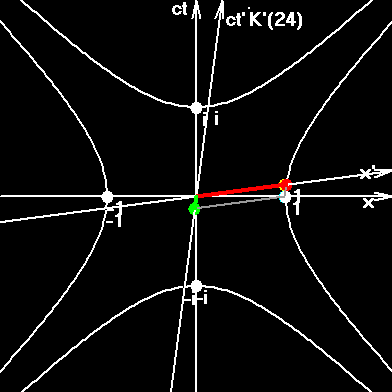
Blue dot. Charge of an electron oscillates along the x-axis. Oscillations are purely harmonic. System K with axes (x, ct).
Red dot is the same charge, but projected into a system K(j). Here it is not just a charge, but rather a field, an element of electron's field. It jumps successively from one IFR to the next IFR, and we can see the Red-dot rotation. Position of red dot can be computed as x' under Lorentz transformations.
Green dot - time t'.
Yellow dot shows the value of quantum velocity.
Imagine a sphere of radius r. It rotates along circumference R=137.036r. You will have torus. But here we have two "but".
1. Sphere of radius r is made in the plane (x, ct) of Minkowski space. So, we have no sphere, but pseudo-sphere, constructed by two hyperboles. Look at the upper figure: two hyperboles which are the trajectories of a Red-dot. In every one full rotation in (x,it) our figure are turned by 1/137.036 fraction of a full rotation in (y,z).
2. Received torus in not the ideal torus. Cut it and shift it's ends along the time axis on the value slightly less then R/137.036. So the next torus will lay on the first one and so on. You have now a double-helical tube.
If an electron will be captured by a proton, the double-helical tube will transform into a triple-helical tube. It's greatest radius will be 137,036*R.
Rydberg constant gives us one more ladder step in this fractal structure of space-time at atomic level.
Today, the 17-th of June, 2018, this page is under updating. Come here again latter.
Here are the most popular transformations:
(1)
x' = (x - vt) / sqr(1 - v2/c2);
t' = (t - vx/c2) / sqr(1 - v2/c2),
where: v = vt - coordinate velocity.
Using sqr(1 + vt2/c2) = 1/sqr(1 - v2/c2) = g, and vt = vg, we'll have:
(2)
x' = xg - vtt;
t' = tg - vtx/c2.
Using g = chy and vt/c = shy, we'll have:
(3)
x' = x chy - ct shy ;
ct' = ct chy - x shy.
(4)
x' = x ch(r/c)
- ct sh(r/c)
;
ct' = ct ch(r/c) - x sh(r/c).
Using cos iy = ch y and sin iy = i sh y, we'll have:
(5)
x' = x cos iy + ict sin
iy
;
ict' = ict cos iy - x sin
iy.
Compare these transformations (turn in the complex space-time) with usual turn in Euclidean space:
x' = x cos j
+ y sin
j ;
y' = y cos j - x sin
j.
On the bottom figure one can see the turn in the complex space-time. The main difference of pseudo-Euclidean turn from the Euclidean turn is the fact that the pseudo-Euclidean axes move towards each other.

Fig 2. Pseudo-Euclidean circumference. This circumference is torn in four points. In fact here we have two pseudo circumferences, described by equations x2+(ict)2=1; x2+(ict)2=-1. The interval from the center of the figure to any point of the right or left hyperbole is equal to 1. The interval from the center of the figure to any point of the upper or bottom hyperbole is equal to i. The interval from the center of the figure to any point of asymptotes, painted in red, is zero. Rapidity parameter y is numerically equal to the length of the arc of a pseudo circumference, painted in dark-green. The length of right arc has the imaginary value iy. The length of upper arc has the real value y. The value y is also equal to the doubled surface of the figure painted in gray color. The figure is built for the velocity v=0,6c. Yellow lines show the world strip of the one-meter moving rod. The slope of the lines corresponds to constant time in the moving system. The ratio v/c is an orange segment. Proper velocity vt is denoted by the small letter b.
Using the formula tgf = thy, we can write one more form of one and the same space-time transformations:
(6)
x' = (x - ct tgf) / sqr(1-tg2f);
ct' = (ct - x tgf) / sqr(1-tg2f).
Special Relativity is not the quantum theory. In this work (Space Genetics) there was supposed that the velocity of elementary particle cannot have continuous spectrum of values. Velocity can change by small portions. Nonzero rest mass particle cannot have no zero velocity, no velocity of light. Macroscopic object can have zero velocity, because it consists of the variety of particles. Let it has two particles. If one particle moves with minimal possible velocity in one direction, and if another particle moves with the same velocity in the opposite direction, then this two-particle object has the zero velocity. This two-particle object we also can name the elementary particle. But in order to avoid contradictions, let's say, that it is a composite object. Moreover, in this work it was supposed that the elementary particle is composite itself. It lives by flashing. Two or three defect links of the space-time lattice move by quasi-closed circumferences with c-velocity and collide one another. At the times of their collisions the particle is materialized. In the period between collisions the particle does not exist. Massless elementary particles (photon, graviton, and may be neutrino) move with velocity c, and are defect links themselves. That is way it is better to name them no elementary particles, but the defect links of the space-time lattice, or shortly, - links.
In 2007 I had made the program of moving electron. Look it in order to better understand the bottom text.
After I have read the book "Four-dimensional world of Minkovskij" (the author Sazanov A.A.) and I asked myself:
1. Can something material move along pseudo-circumference?
2. How many pseudo-circumferences are made by these four hyperboles?
Now I can answer.
1. Yes. This rotation corresponds just to my old model of elementary particle, consisting of a set of quasi closed circumferences. Earlier I imagined them in the curved space with positive curvature, and now I see a particle as a set (2-3) of quasi closed circumferences, and at least one circumference of the set is pseudo-euclidean.
2. Four hyperboles give two pseudo-circumferences. The first pseudo-circumference has the radius r, is composed from left and right hyperboles. Its relativistic length is equal to 2pri, where i is a square root of minus one. The second pseudo-circumference is made from bottom and top hyperboles. It has the radius ir. It's relativistic length is 2pr.
Let in a point x=0 there is a transparent positive elementary charge. Let electron move along the straight line between points x1 = -R; x2 = R. Electron constantly changes it's velocity and as a result, it constantly changes the reference frames. Axes turn and draw same curves. Numerical modeling had shown, that in order the image of electron draw the ideal pseudo-circumferences, it must to start its dropping on positive charge from R=rcl, there rcl is the classic radius of an electron.
Let's make more precise terminology. Let along the axis moves the electron itself. Let electron's images or links move along hyperboles. Further we'll see that moving links draw circumferences around the point x=0 and ict=0. Pay attention: ict=0 constantly.
Velocity of electron changes from zero to velocity of light. But what is the velocity of links? At the period of one full rotation they run over the whole Universe. Absurd? No. They move not only in space, but in space-time. We must take into account the relativistic length. Every small part of hyperbole must be divided by coefficient
g = chy = 1 / (1- (v/c)2)1/2.
Thus we will have relativistic length of element of upper or bottom hyperbole: dl = rcldy/chy. Taking the integral from 0 to infinity we'll have prcl/2. That is the relativistic length of one half of this hyperbole. The whole rotation of one link of electron takes two hyperboles and it covers the relativistic length l1 = 2prcl. The second link of electron moves on right and left hyperboles and covers the relativistic length l2 = 2pircl.
Let radius of rotation will be equal to 1, then we will can receive the angle Q = oIy dy / chy which can named the parameter of quantable velocity. And as a result we can introduce the quantable velocity vq itself, which can be received from equation vq/c = Q. The value vq has minimum vq_min=-pc/2 under Q =-p/2; and maximum vq_max=pc/2 under Q =-p/2.
It is not difficult to receive the following connections:
x = rclcosQ; ict=rclsinQ.
Seventh type of space-time transformations:
x' = (x - ct sinQ)/cosQ;
ct' = (ct -x sinQ)/cosQ.
Connections between different types of velocities:
vt/c = sinQ = sin(vq/c);
vt/c = tgQ = tg(vq/c);
g = 1/cosQ= 1/cos(vq/c);
vt/c = thy = th(vy/c);
vt/c = shy=sh(vy/c);
g = chy=ch(vy/c);
th(y/2) = tg(Q/2).
thy=tgf,
tg(p/4 + Q) = (tg(p/4 +
f))1/2.
Look, it's beautiful:
dv/dt = g0dv/dt;
- - - - - - - - - -
dvq/dt =
g1dv/dt;
dv/dt =
g1dv/dt;
dvy/dt =
g2dv/dt;
dvq/dt =
g2dv/dt;
dvt/dt =
g3dv/dt;
dvy/dt =
g3dv/dt;
- - - - - - - - - - ; dvt/dt
= g4dv/dt.
More in my Russian-language pages 10, 11.
Let's receive the minimal and maximal values using N, - the big quantum number of space-time lattice.
Qmin = Q1 = oIy1 dy / chy = (p/2) / N = p / 2N.
Q2 = oIy2 dy / chy = p / 2N + p / N = 3p / 2N.
Q3 = oIy3 dy / chy = p / 2N + 2p / N = 5p / 2N.
Qn = oIyn dy / chy = p / 2N + (n-1)p / N = (2n-1)p / 2N.
Qmax = (N -1)p / (2N) = p / 2 - p / 2N.
Using: tg(Q/2)= th(y/2)
yn = 2Arth(tg(Qn/2)) = ln((1+tg(Qn/2))/(1-tg(Qn/2))) = ln(tg(p/4 + Qn/2))
ymin = p / 2N,
ymax = ln(4N/p).
Using: v=c sinQ
vn = c sinQn= c sin((2n-1)p / 2N).
vmin = cp / 2N.
vmax /c = sinQmax = sin(p
/ 2 - p / 2N) = cos(p / 2N)
=
= (1- (sin(p / 2N))2)
1/2 = (1-
(p / 2N)2)
1/2 =
= 1 - p2 / 8N2.
Using: vt=c tgQ
vt,n = c tgQn = c tg((2n-1)p / 2N).
vt,min = c tg(p / 2N) = cp / 2N.
vt,max /c = shymax
= sh(ln(4N/p)), Arsh(vt,max
/c) = ln(4N/p),
ln(vt,max /c + ((vt,max
/c)2 +1)1/2) = ln(4N/p)
vt,max/c = 2N/p.
Using: g = 1/cosQ = chy
gn = 1/cosQn = 1/cos((2n-1)p / N).
gmin = 1/cosQmin = 1/cos(p / 2N) = 1 / (1 - p2 / 8N2) = 1 + p2 / 8N2.
gmax = 1/cosQmax = 1/cos(p/2 - p / 2N) = 1/sin(p / 2N) = 2N/p.
If gmax = 2N/p, then:
rcl' = rcl / (2N/p),
rcl' = (e2 / (4pe0mc2)) / (2(ap / df)1/2/p),
rcl' = (hG / 8c3)1/2.
Classic radius of electron, moving with maximal possible velocity, is equal to Plank length with slightly different coefficient. Compare:
rPl = (hG / 2pc3)1/2.
Analogously we can receive the value for relativistic mass of an electron, moving with maximal possible velocity
mr = m0 2N/p.
mr = (a/p)(2hc / G)1/2.
Compare:
mPl = (hc / 2pG)1/2.
One more conclusion: For observer, moving with maximal possible velocity, the Universe will look contracted to graviton-photon boundary wave-length, l0p/2.
This observer will cross it by the boundary time
t = (l0p/2) / vq.max = (l0p/2) / vq.max = (l0p/2) / (cQmax) = l0/c = t0.
Back to part 1: Three types of velocities. Rapidity parameter y and rapidity r.
Back to part 2: Interval. Four-dimensional velocities. Types of acceleration. Four-accelerations. Relativistic rocket.
To index of Space Genetics.
Ivan Gorelik