Эти детские задачки загонят вас в тупик.
Дуализм понятия скорость.

Здравствуйте, уважаемый читатель! Надеюсь, что Вы знаете азы Специальной Теории Относительности (СТО).
Если да, то попытайтесь быстро решить Задачу:

Вы сделали идеальный метровый стержень. Предположим, что он скользнул, извиняюсь, по Вашему носу точно за одну секунду.
Чему равна его скорость?

Варианты ответов:
1) 1 м/с;
2) меньше 1 м/с;
3) больше 1 м/с.

Отвечайте быстро! И большинство из вас скажет: "Скорость стержня равна одному метру в секунду".

Увы, ответ неправильный.

Если вспомнить курс средней школы, то вам говорили в старших классах, что продольные размеры движущихся тел сокращаются. Значит, стержень который пролетал мимо Вас уже был не метровый, а укороченный. А чтобы узнать его настоящую скорость, необходимо определить, на сколько же переместится какая-то его точка, к примеру его начало, за секунду. Это мы вычислим чуть ниже. А сейчас давайте задумаемся - а что же мы вычислили, как не скорость. Ведь стержень длиной точно метр, чиркнул но носу точно за секунду. Это было реально. Это мы прочувствовали физически. Что же это за величина?

На самом деле Вы нашли физическую величину, которая почти не используется в физике. Называется она собственная скорость. В англоязычной Википедии в статье Proper velocity её обозначают буквой w. А букву v оставляют за скоростью, соответствующую её определению в физике, и называют её координатная скорость v.

Давайте вернёмся к решению задачи. Согласно СТО длина движущегося стержня сокращается в γ раз. Изобразим это на рисунке:

На рисунке показано личико игрушечного человечка с белым носом, сделанным из мелка. Движущийся стержень, окрашенный в синий свет, за секунду проезжает по меловому носу, и мы видим меловый след носа на синем стержне. Пускай в передней части движущегося синего стержня закреплен мелок, который с свою очередь оставляет меловый след на покоящемся красном стержне, который был изготовлен в точности такой же длины, как и синий стержень. Поскольку синий стержень сокращён и чиркал по носу в течении секунды, то его скорость можно узнать делением длины следа, оставленного синим стержнем на красном стержне, на одну секунду.

v = d/t.

Выше мы указали, что длина движущегося стержня сокращается в γ раз. Этот коэффициент называется лоренц-фактором, который был известен ещё до создания теории относительности:

γ=1/√(1-v²/c²)

Чтобы получить длину сокращенного стержня делим исходную длину на лоренц-фактор:

d = d₀ / (1 /√(1-v²/c²)) = d₀ · √(1-v²/c²)

Подставим это в формулу для нахождения v:

v = d₀ · √(1-v²/c²) / t.

Скорость входит и в правую, и в левую часть уравнения. Проделав выкладки, получим:

v = w / √(1+w²/c²).

В полученной формуле буквой w = d₀/t = 1м/с мы обозначили собственную скорость, которую получили вначале и по ошибке приняли за координатную скорость. Подставляя данные, получим значение координатной скорости:

v = 0,99999999999999999443674972... м/с.

Очень близко к единице, но не единица. Следовательно, несмотря на то, что идеальный метровый стержень скользил по носу точно одну секунду, координатная скорость стержня оказывается чуть меньше одного метра в секунду.

Кроме того, мы можем заметить симметрию. Оказывается, лоренц-фактор, может быть выражен подобным образом через оба вида скорости:

γ = 1/√(1-v²/c²) = √(1+w²/c²)

Задача 2.

Идеально ровная дорога. Вы проезжаете километровый знак "100". На ваших часах 12.00. Вы проезжаете километровый знак "200". На Ваших часах 13.00. Чему равна Ваша скорость?

Кто сказал: "100 км/час точно", тот ошибся. Мы здесь снова столкнулись с собственной скоростью. Эта задача решается аналогично. Роль стержня выполняет идеально ровная дорога, которая тоже будет сокращаться относительно вашего автомобиля. Либо, если бы Вы смотрели не на ваши часы, а на синхронизированные часы, связанные с километровыми знаками, то вы бы "заметили", что показания ваших часов и часов на километровых знаках отличаются тем больше, чем дальше Вы продвигаетесь с постоянной скоростью. Я написал в кавычках, поскольку это отличие очень мало, и фактически мы бы не смогли его увидеть. Это был мысленный эксперимент с идеальными часами и с идеальными возможностями наблюдателя.

Если нет желания возиться с выкладками, то задачу можно решить по действиям:
1) найти собственную скорость, w = d₀ / τ, где τ - время движения по Вашим часам,
2) найти лоренц-фактор γ = √(1+w²/c²);
2) найти координатную скорость; v = w /γ.

Чтобы не путаться, следует помнить, что лоренц-фактор всегда больше единицы. Значит он равен отношению большего на меньшее: собственная скорость больше координатной; длина покоящегося стержня больше длины движущегося стержня...

Задача 3.

Вы в звездолете. Фотонный двигатель Вашего звездолета имеет неограниченные технические возможности, но теория относительности верна. Перед Вашими глазами карта галактик. У вас есть часы. Вы пролетаете между двумя галактиками, расстояние между которыми равно 10²² метров, за одну секунду. Возможно ли это?

Кто сказал: "Нет", тот ошибся. Действительно, разве может некоторое тело двигаться с координатной скоростью 10²² м/с? Максимум координатной скорости равен 3·10⁸ м/с. А максимум для собственной скорости есть бесконечность. Роль стержня в этой задаче выполняет вся Вселенная, сокращающаяся относительно системы отсчета, связанной с Вашим звездолётом. Если вы разделите 10²² метров на одну секунду, то получите величину, которая на много порядков превышает координатную скорость света? Но имеем в виду, что Ваша ракета движется всё равно медленнее света, поскольку собственная скорость самого света равна бесконечности. Собственные часы фотона, образно говоря, стоят, в силу колоссального замедления времени.

Собственная скорость не менее физична, чем координатная скорость. Как мы увидим далее, обе скорости дополняют друг друга. Это как две стороны одной монеты:
аверс и реверс;
лицевая сторона с гербом и оборотная сторона с номиналом монеты;
орёл и решка.
Если присмотреться, то у монеты есть ещё и гурт - боковая сторона, ребро.
У скорости тоже, помимо двух сторон, есть своё ребро - быстрота. И она, как оказалось, тоже распадается на две удивительно симметричные стороны: тригонометрическую и гиперболическую.

Так почему же разные способы измерения дают разные результаты? Может быть, какой-то из способов нам мерещится? Иллюзорный? Для выяснения этого, давайте решим ещё одну задачу.

Задача 4.

Предположим, что мы сделали релятивистский автомобиль, способный двигаться со скоростями, близкими к скорости света. Какую физическую величину измеряет спидометр этого автомобиля?

Указание: Поскольку при релятивистских скоростях все точки колеса метровой длины обода будут иметь скорость порядка 10¹⁵ м/с, а центростремительное ускорение a=v²/r~10³⁰ м/с², что равно 10²⁹g и соответствует центробежной силе 10³⁰ Н на каждый килограмм обода, то ни один материал не выдержит таких центробежных сил, разрывающих его на части, а значит, мы пренебрегаем деформациями колеса, связанными с центробежными силами. Пренебрегаем также сокращениями продольных размеров автомобиля. Учитываем лишь то, что колесо движущегося автомобиля в точке касания с дорогой покоится относительно дороги. Оно, может оставлять абсолютно недеформированный след на дороге. Если на колесе с метровой длиной обода имеется 40 шипов, то на метре дороги останется рисунок 40 шипов. С другой стороны, каждый пройденный метр дороги соответствует одному обороту колеса, одному обороту тросика, ведущему к центробежному механизму в машине. А стрелка спидометра отклоняется тем сильнее, чем больше оборотов делает центробежный механизм за единицу времени по часам, тикающим в машине.

Варианты ответов:
1) v;
2) w;

Пока вы думаете - информация. В английском языке нашему слову скорость соответствует два слова velocity и spead. В решениях задач за словом spead они оставляют модуль или абсолютное значение velocity. Они не хотят менять устоявшиеся традиции. Что бы вы им посоветовали?

Так что же измеряет спидометр автомобиля?
U-сть (U-locity), или
W-сть (W-locity), а может
Ψ-роту (Ψ-pidity), от быстроты, rapidity
Q-роту (Q-pidity).

Вы наверное уже догадались. Спидометр измеряет собственную скорость w. Произносим с ударением на А: д'аб-сть, англоязычным - dab'i-city. Проиграла 'ю-сть, u-l'ocity Поэтому надо переименовать собственную скорость w в spead, либо спидометр в даб'и-метр. Это было лирическое отступление, но оно проясняет суть.

Скучно? Вот раздвоение скорости электрона,

Вот раздвоение скорости электрона, происходящее поточу что электрон это не точка, а крохотная двухполюсная струна, которая растягивается на всю Вселенную, вращаясь, совершает один оборот вокруг Вселенной за классическое время электрона сжимается опять до классического радиуса электрона и т.д. При этом работает исключительно электродинамика и СТО. Всё просто.

При этом не нарушая ни одного постулата СТО. С причинно-следственными связями всё ОК. НО!!! Теория близкодействия, царствовавшая с момента творения поля, подвергается нападению со стороны дальнодействующей даби-сти, реагируя на поля ближайших тел и самых далёких галактик прошлого, и оставляя о себе памятку на будущие события рядом и на далекие галактики будущего. При этом мировая линия электрона всегда времени-подобна.

Почему он так быстро облетает эти миллиарды световых лет - спросите вы. Потому что его траектория лежит почти на диагонали, а там элементы интервала близки к нулю. Давайте покажу, как получается ноль. Возьмём две точки на диагонали и подсчитаем "гипотенузу".

AB = √(5²+(i·5)²) = √(25+25i²) = √(25-25)=0.

Поскольку он летит не точно по диагонали, а приближаясь к ней асимптотически, его пройденный путь не равен нулю, а 2πr_cli, где: r_cl - классический радиус электрона, i - корень из минус единицы. Появляется вследствие того, что он движется по времени-подобной траектории. Он вращается не в плоскости (x, y), а в плоскости (x, ict).

- А могут ли так быстро облетать Вселенную люди?

- Так быстро не получится. Но за пару лет можно, теоретически. Нужен двигатель на 1000 кВт. Это мелочи! Сравнимо движку вашего автомобиля. Реактивный, который выбрасывает не отработанное топливо, а продукты распада вылетающие из ядерного реактора. Такого двигателя пока нет. Кроме того, окостеневшая наука, не хочет знать, что такое собственная скорость...

ПЕРЕРЫВ. Завтра продолжим.

ведь вектор скорости можно представить в виде Фактически в природе существует два вида измеримых скоростей, основанные на разных методах измерения. Поскольку обе эти скорости измеримы, то значит они обе реальны. Измеримость здесь следует понимать в более широком смысле: речь идет не просто об измерении скорости с помощью линеек и часов, а воздействуем одного объекта на другой объект, со всеми вытекающими физическими последствиями. Взгляните еще раз на рисунок, и мысленно прочувствуйте два вида скорости.

Всё дело в том, что физическая величина под названием скорость является не только многокомпонентной, как вектор, представленный его проекциями:

v = v_xi + v_yj + v_zk,

но и многогранником, имеющим 4-е стороны или вида:

V = (U, Q, Ψ, W).

Как мы увидим в последующих разделах, здесь появляется не только раздвоение результатов при разных способах измерения, но и раздвоение самого объекта измерения. В физике уже есть аналогия раздвоения скорости. Это наблюдается при изучении распространения электромагнитных волн, кванты которых считаются безмассовыми частицами, а также при наблюдениях волн Де-Бройля, связанных с элементарными частицами, имеющими массу. И там, и там фазовая скорость исследуемого объекта может превышать скорость света. При этом утверждается, что фазовая скорость не является переносчиком энергии и информации. Другими словами, нет нарушения причинно-следственных связей. Может быть, в исследуемом нами многограннике скорости есть связи с фазовой и групповой скоростью, но пока-что я вижу лишь аналогии: раздвоение, превышение скорости света одной из компонент раздвоившегося объекта. Уточнимся, поскольку мы уже знаем, что нет никакого превышения, поскольку для света тоже есть два предела:
v_{света макс.}=с; и w_{света макс.}=∞. Для того, чтобы обогнать свет, необходимо одолеть его по обоим пределам для света, с и ∞, а последнее означает, что обгоняющий объект должен двигаться со скоростью больше бесконечности.

Выбрасывать собственную скорость из физики подобно отказу от косинуса в геометрии; а точнее, из теории относительности был выброшен синус гиперболический sh от быстроты Ψ, дающий собственную скорость: w=c·shΨ=c·sh(v_ψ/c), где Ψ, или v_ψ - параметр скорости, или быстрота, который можно выражать в "угловых"* единицах вот здесь: Ψ, и в метрах в секунду вот здесь: v_ψ. Быстрота уже известна в физике более сотни лет. А собственную скорость w, получаемую взятием гиперболического синуса от быстроты, пренебрегают.

Собственную скорость w можно также получить путём взятия тангенса от квантовой скорости Q: tgQ=tg(v_q/c)=w/c, где Q, или v_q - четвертая сторона такой многогранной монетки, под названием скорость v. Четвёртый вид скорости тоже может быть выражен в радианах здесь: Q, и в метрах в секунду вот здесь: v_q. Этот вид скорости я назвал квантовой скоростью. С ней наверняка работали другие физики, но я пока не нашёл информации по этому поводу.

Не так давно я узнал, что функциям Ψ и Q, используемым здесь, есть потрясающие аналоги, которые были получены ещё в 18-19 веках. Это функции Ламберта и Гудермана, иногда обозначаемые так: lamΨ и gdφ. О скоростях там не говорится ни слова, но почти все формулы для кинематики СТО, там уже были написаны, включая лоренц-фактор, с помощью которого, мы решали задачи вверху. Лоренц-фактор выражается потрясающе элегантно через величины Ψ и Q:

γ = chΨ = 1 / cosQ

А значит можно записать связи между 4-мя сторонами скорости:

w = v / cosQ = v · chΨ.

Если "углы" выражать не в радианах, а в метрах за секунду, то:

w/c = (v/c) / cos(v_q/c) = (v/c) · ch(v_Ψ/c.

Много скоростей?
Не пугайтесь. Все эти скорости есть лишь функции единого темпа движения. Аналогичная картина складывается в геометрии. Есть угол поворота. И есть функции угла поворота: sin, cos, tg, ctg... Координатная и собственная скорость измеримы, а быстрота и квантовая скорость легко вычисляемы. Хотя я не исключаю, что сейчас существуют способы их измерения. Достаточно лишь знать, какой физический эксперимент нам напрямую указывает на эти самые углы*.

Кто-то подумает, - А стоит ли читать это дальше?

- Да. Ибо в одном случае, отслеживая элементарную частицу из системы К, мы видим её как точку, а в другом случае - как вращающуюся и растягивающуюся / сокращающуюся струну. Приведённый пакет формул помогает нам построить модель электрона, не просто как частицы, а как некой тройственности, ибо он есть и
1) частица, и
2) электромагнитное поле, простирающееся на всю Вселенную на 13 млрд. световых лет во все стороны по пространственным координатам, и на 13 млрд. лет во времени в прошлое и будущее, и, наконец, электрон ещё и
3) элемент пространства, как осциллятор, струна, вибрирующая и вращающаяся в пространстве-времени Вселенной, являющаяся пристанищем для пульсаций других частиц/волн. Тот, кто читал квантовую механику наверняка слышал, что корпускулярно-волновым дуализмом обладают не только фотоны, но и все элементарные частицы, из которых мы состоим. После тщательного разбора v-скорости и w-скорости у меня сложилось впечатление, что причиной корпускулярно-волнового дуализма частиц является дуализм скорости. С одной стороны её пределом является конечное значение, а с другой - бесконечность, или некоторое другое конечное значение - очень большое, но конечное. Предположим, что очень медленно растущая величина ψ имеет предел равный постоянной тонкой структуры1/α ~ 137,036. Тогда максимальное значение собственной скорости в долях скорости света можно вычислить так:

w_max = shψ = 1,6329·10⁵⁹.

К размышлению:
e^137,036/2=1,6328587823117754388281176498021·10⁵⁹
sh(137,036)=1,6328587823117754388281176498021·10⁵⁹
1/(1-th(68,518))=1,6328587823117754388281176498021·10⁵⁹

Давайте разберём кусок из моей программы о связях между V-скоростью, даби-скоростью и параметрами. Для начала лишь поверхностно. А более детально разбёрём её в последующих разделах.

Программа для сравнения различных видов
на одну и ту же скорость.

Я ввожу значение двух величин: угол Q и число допустимых сонаправленных скоростей в одном и том же направлении x. Всё остальное вычисляет компьютер.

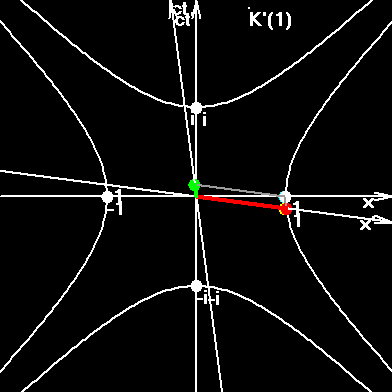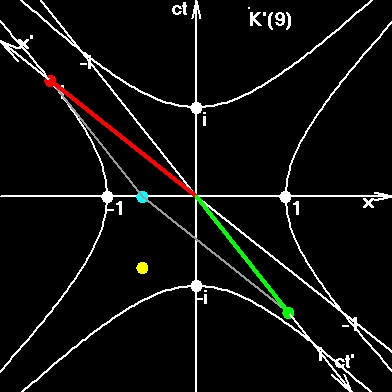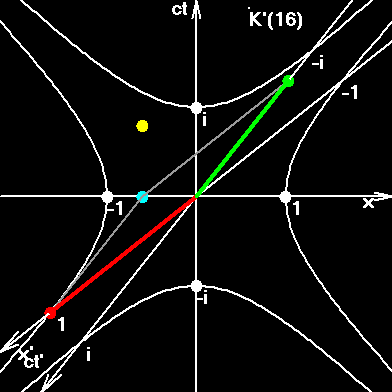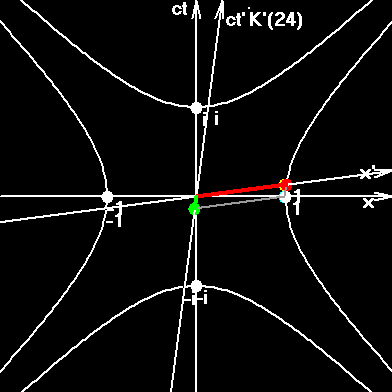
Я задал очень маленькое число возможных значений для квантовой скорости. Всего лишь 24 на интервал от 0 до π/4. То есть, Q₁= π/96, второе в два раза больше, третье - в три... Q₂₄= π/4. Другие виды скорости машина вычисляет по формулам. Кусок гиперболы нарисован не плавно, а представляет собой ломаную из 24 отрезков, представляющих собой приращения для следующей быстроты. То есть, 24-я быстрота есть комплексная длина всей ломаной линии, напоминающей кусок гиперболы.
24-ая квантовая скорость соответствует длине дуги на окружности, начинающейся на горизонтальной оси, и оканчивающейся в точке пересечения с зелёным отрезком в точке V₂₄. V-скорости показаны зелёным цветом.
W-скорости показаны синим цветом.
Ψ-скорости - соответствующие дуги на гиперболе.
Q-скорости - дуги на окружности.

Дуализм понятий скорость и быстрота.

Человек, читающий текст по диагонали, не заметит слова собственная , но услышав фразу какая-то скорость в десять раз больше скорости света, акцентирует своё внимание на этом куске фразы, и прекратит слушать собеседника, приняв его за очередного опровергателя теории относительности. Это одна из причин написания этого раздела. Здесь СТО не опровергается, а напротив мы ищем новые связи. А главной причиной написания этого раздела является то, что, скорее всего, в основе корпускулярно-волнового дуализма частиц лежит дуализм скорости. Давайте вникнем детальнее.

В силу того, что терминология и обозначения в этой области физики плавно меняются, и у разных авторов отличаются, я попытаюсь обобщить то, что мне известно, и предлагаю ниже свой вариант. В англоязычной Википедии лет 15 назад появилась статья о собственной скорости, Proper velocity. Сейчас её отредактировали и один из авторов через-чур замусорил её своей тематикой, не относящейся к теме. В русско-язычной Википедии появлялась статья о ней же, но под названием Правильная скорость. Сейчас (28.01.2026) статьи нет. А в конце 90-х, начале нулевых я "выносил мозги" нашим и англоязычным физикам, что надо либо вводить понятие собственной скорости, называя её к примеру spead потому что спидометр нашего автомобиля измеряет не v-скорость, а w-скорость, предел которой равен бесконечности, либо надо переименовать спидометр. В ответ меня лишь оскорбляли, утверждая, что Ваша скорость неправильная. Я доказывал, что она правильная. В итоге у них появилась статья Proper velocity, а у нас на время возникла статья Правильная скорость.
- Ну не бред ли? Поэтому вот предлагаемая терминология и картинка дуализма.

СТОР! ПЕРЕРЫВ. Редактирование продолжим чуть-чуть позже. Сейчас 22:00. 2 февраля 2026. Загляните сюда через денёк.
Уважаемый читатель! Если Вам что-либо известно о видах скорости W и Q, просьба сообщить мне об этом по адресу darkenergy@yandex.ru Желательно с указанием на источник. Не может быть, чтобы американцы были первыми в плане введения W. Не может быть, что бы я был первым, кто обратил внимание на величину Q, как элемент единого понятия скорости.

(*) Я обозвал единицы измерения аргумента гиперболических функций радианами. На самом деле там ситуация гораздо круче. Эту ситуацию как раз и проясняет выше введенный пакет из четырех видов одной и той же скорости. На самом деле аргументом гиперболических функций является не угол и не длина дуги гиперболы, а удвоенная площадь кривого сектора, образованного дугой гиперболы и двумя лучами исходящими из точки (0, 0). Математики 18-го века не знали о сокращении длин, следующих из теории относительности, созданной в начале 20-го века. Но если бы они разделили каждый элемент гиперболы dψ на соответствующий лоренц-фактор chΨ, то полученную укороченную длину дуги ₀∫^Ψdψ/chΨ можно было бы назвать "релятивистской длиной дуги", численно совпадающей с длиной соответствующей дуги на окружности. При этом не надо было бы прибегать к удвоенной площади кривого сектора. Не надо было бы нам "пудрить мозги" и говорить: Вон, смотрите, - для окружности единичного радиуса мы получаем один и тот же результат, если впишем в качестве аргумента любую из вот этих трёх величин:
1) центральный угол опирающийся на дугу, выраженный в радианах;
2) отношение длины дуги окружности к радиусу;
3) удвоенное отношение площади сектора к площади круга.

В случае гиперболы работает только третье. Второе будет работать, если в качестве длины дуги брать не видимую нами длину, каждый элемент которой определяется по теореме Пифагора ds²=dx²+dy², а комплексную, для которой работает не сумма катетов, а разность: ds²=dx²-dy², а, если сумма, то один из катетов должен быть мнимым: ds²=dx²+(i·dy)².

Если Вы не верите тому, что я сказал, то посмотрите в Википедии статью о гиперболических функциях. Выясните, что там идёт в качестве аргумента для гиперболических функций. Кстати, а Вы не задумывались, почему обратные гиперболические функции мы озвучиваем так: "ареасинус гиперболический", а не "арксинус", как для круговых функций. Ответ из той же оперы - там в качестве аргумента используется не дуга arc и не угол, а удвоенная площадь area кривого сектора, образованной куском гиперболы и двумя лучами, идущими из точки (0, 0). Длина дуги не соответствовала ожиданиям, а лоренц-фактор основательно пришёл в науку лишь после публикации первых работ Эйнштейна.

Вот как мы пишем обратные тригонометрические функции:
arcsin, arccos, arctg, arcctg - с приставкой arc, дуга; а гиперболические так:
arsh, arch, arth, arcth по-русски, с приставкой ar от слова area, и вот так:
arsinh, arcosh, artanh, arcoth по-английски, тоже с приставкой ar. Программисты экономили место на реальном калькуляторе, и на виртуальном, который есть на рабочем столе вашего компа или гаджета, и ввели для обратных функций показатель ^-1:
sinh^-1, cosh^-1, tanh^-1, coth^-1. Это нововведение переползло в научные статьи, т.к. молодёжь предпочитает гаджеты вместо книг. В результате сейчас путаница преумножается, ведь y^-1 есть 1/y, а не функция, обратная y.

(**)По поводу слова вид скорости. В данном случае слово вид предпочтительней слова компоненты по двум причинам:
1) компоненты уже задействованы проекциями вектора v;
2) в быту мы иногда употребляем выражения вид в профиль, в анфас, а в черчении - вид спереди, вид сбоку, вид сверху. В случае со скоростью мы имеем вид K - из покоящейся системы координат, вид τ - измерение скорости движения тела, дороги, космических объектов пространства относительно нас по собственным часам, вид ψ, вид Q.