Расчет Магнитной Дыры.
Теория магнитной дыры пока что отсутствует в курсе физике, но магнитная дыра может быть создана на коллайдере и уничтожить всех нас.
В этой колонке изложены два подхода для выяснения физических характеристик минимальной магнитной дыры, способной разрушать протоны. Первый подход, названный Вложение Нуклонов, получен в сентябре прошлого года и уточнен в начале этого года. Второй подход, названый Создание Магнитной Дыры, исследован в марте, апреле 2009-го. Он основан на компьютерном моделировании столкновений протонов и уже дал некоторые результаты, совпадающие с результатами первого подхода.
В правой колонке (16-25 апреля 2009) изложен третий подход Характеристики Магнитной Дыры. Он дает подобные результаты, распадается на несколько ветвей, и дает новые результаты, к примеру, собственные частоты магнитной дыры, примерно совпадающие с наблюдаемыми частотами пульсаров.
Первый подход. Вложение Нуклонов.
Вводное приложение к первому подходу.
Для того, чтобы был понятен первый подход, проследите за поведением
массы.
Образование магнитной дыры подобно «лепке» ядер из нуклонов.
Пускай масса нуклона (протона или нейтрона) состоит из двух частей: полевой
массы и конденсатной массы (массы нуклонных остатков).
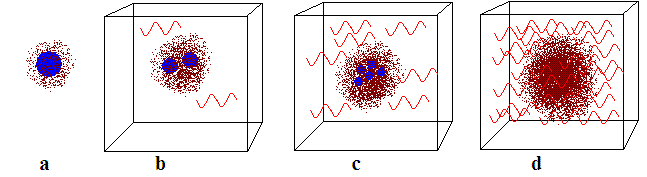
Смотри рисунок а: полевая часть изображена множеством коричневых
точек; конденсатная масса - синим кругом. С полевой массой можно связать
поле пи-мезонов (или поле глюонов в более современной интерпретации). С
конденсатной массой можно связать массу голого нуклона (или суммарную массу
кварков).
При слиянии двух нуклонов (протона и нейтрона), как известно, полная масса
образовавшегося ядра будет меньше полной суммы масс протона и нейрона. Разность
масс между конечным и начальным состоянием указывает на энергию связи образовавшегося
ядра. Если пренебречь кинетическими энергиями частиц до и после реакции,
то можно сказать, что энергия связи равна энергии фотонов, излученных во
время реакции, и показанными на рисунках волнистыми линиями. Мы можем учесть
массу, связанную с излучением, помещая соединяемые нуклоны в ящик с идеально
отражающими стенками. Тогда мы получим равенство масс в правой и левой частях
уравнения.
Соединяя нуклоны вместе, мы заметим, что конденсатная масса образующегося
ядра будет меньше, чем сумма конденсатных масс нуклонов, вступающих в реакцию.
А полевая масса образующегося ядра будет больше, чем сумма полевых энергий
нуклонов. Кроме того, наш ящик будет наполняться фотонами, излученными во
время реакции. Смотри рисунок b и c, где синие круги, отображающие
конденсатную массу, становятся все меньше с ростом количества нуклонов в
ядре, а густота коричневых точек, отображающая полевую массу, становится
всё гуще.

Если бы в ядре существовали только ядерные силы, то наступил бы момент,
когда конденсатная масса обратилась бы в ноль. Это схематически изображено
на рисунке d, где радиус синих кругов стал равен нулю, - их просто
уже нет. Но, как известно, с ростом числа протонов в ядре, растут электростатические
силы отталкивания. И из-за этого существует «железный пик» в энергии связи
на нуклон, и существует предельный элемент таблицы Менделеева. Если бы не
было электрических сил отталкивания, то все нуклоны бы свалились в «ядерную
дыру», не имеющую предела роста.
Образование магнитной дыры подобно росту ядерной квази-дыры (росту ядра
при его синтезе из легких ядер). Протон, "проваливающийся" в магнитную дыру,
теряет позитрон, а нейтрон теряет антинейтрино.
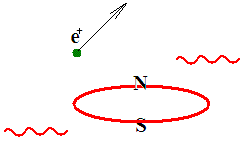
Согласно Стандартной Модели протон состоит из трех кварков (uud), и может
быть представлен, как три материальных шарика на непрерывном континууме
пространства-времени. Согласно нашему подходу континуум пространства-времени
не является непрерывным, а протон есть некоторый узел, образованный потоком
самого пространства времени. Этот поток создает три полюса, подобно тому,
как электрический кольцевой ток создает два магнитных полюса: N, S. Полюса
протона и нейтрона являются не чисто магнитными, а смешанными, то есть,
несущими и магнитный, и электрический заряды и слабый заряды. Обозначить
эти полюса мы можем точно так же как обозначены кварки, но представление
теперь об этих кварках-полюсах у нас совершенно другое: "Протон не состоит
из трех кварков (uud), а имеет три полюса (uud)". Аналогия: "Постоянный
магнитит не состоит из двух частей, Северной и Южной, а имеет два полюса,
Северный и Южный".
Учитывая, что полюса u и d создаются движением некоторой пространственно-временной
субстанции вдоль нитей узлов, протон и нейтрон схематически можно изобразить
в виде некоторых токовых узлов с полюсами u, u, d для протона:
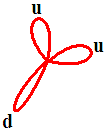 , и d, d, u
для нейтрона:
, и d, d, u
для нейтрона: 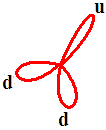 .
.
При попадании в мощное магнитное поле, токовые узлы подвергаются распрямляющим
силам. Чем больше поле, тем больше распрямляющие силы, тем меньше конденсатная
масса нуклона, и тем больше его полевая масса. Наконец, если поле достаточно
сильно (~1016 Тл), то нуклон разрушается; его трехполюсный узел
разделяется на два двухполюсных узла, - позитрон и х-бозон. Позитрон является
электрическим однополюсником, но магнитным двхполюсником. Х-бозон, вероятно,
является и электрическим и магнитным двухполюсником. Позитрон покидает область
сильного магнитного поля, а х-бозон входит составной частью в область намагниченного
вакуума, увеличивая размер этой области. Область намагниченного вакуума
можно назвать магнитной дырой. Энергия связи магнитной дыры и её нового
х-бозона равна энергии, выделенной во время его захвата. Часть этой энергии
является кинетической энергией выброшенного позитрона, а вторая часть уносится
гамма-квантами.
Ниже мы говорим о двух видах распадов: бета-распадах и барионных распадах. Иногда говорят, что распад протона может быть впервые осуществлен на Коллайдере. Во избежание недоразумений и путаницы с бета-распадами, распаду протона, ожидаемому на Коллайдере, мы добавим приставку барионный. При этом подразумевается, что во время такого распада барионное число уменьшатся на единицу. Лептонное число при этом тоже уменьшается на единицу. Таким образом, если согласно модели Большого Взрыва, в Начале происходил бариогенез, то на Коллайдере может быть запущен бариоцид.
Примеры бета-распадов:
n = p + e- + ν~;
p = n + e+ + ν.
Нейтрон в свободном состоянии испытывает бета- распад. В стабильном
ядре нейтрон не распадается. В нейтронно-избыточном ядре нейтрон испытывает
бета- распад. Свободный протон не испытывает бета+
распад, поскольку масса продуктов бета+ распада превосходит массу
протона. В нейтронно-дефицитном ядре протон может испытывать бета+
распад. Некоторые нестабильные ядра могут испытывать и бета-
распад и бета+ распад. К примеру:
K40 = Ca40 + e- + ν~;
K40 = Ar40 + e+ + ν.
Поскольку нейтрон и протон имеют одно и то значение барионного заряда, равного
единице, в бета распадах барионное число сохраняется.
В барионном распаде барионное число не сохраняется, если его не приписать магнитной дыре, - поглотителю продуктов распада нуклонов. Схематическое изображение преобразования протонного трехполюсника в два двухполюсника, - e+ и х-бозон:
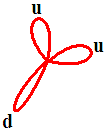 ----->
-----> 
Нейтрон, будучи трехполюсником (udd), в сильном магнитном поле может испытывать подобный распад на два двухполюсника, - антинейтрино и х-бозон:
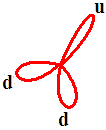 ----->
----->

Поскольку магнитный момент нейтрона отрицателен, он может быть вытолкнут из области сильного магнитного поля. Поэтому вероятность барионного распада нейтрона меньше, чем вероятность барионного распада протона. Если вещество планеты или звезды испытывает магнитный коллапс, то протоны испытывают барионный распад, а нейтроны оказываясь в избытке испытывают бета распады: n = p + e- + ν~. Образующиеся при этом протоны втягиваются в магнитную дыру, где испытывают барионный распад. Электроны, образующиеся в бета распаде нейтронов аннигилируют с позитронами барионных распадов протонов. Часть позитронов и электронов могут выбрасываться растущей магнитной дырой в противоположных направлениях, образуя радио-выбросы, которые наблюдаются в космосе.
Если магнитная дыра имеет большую массу, то помимо магнитного поля она обладает сильным гравитационным полем. Магнитное поле дипольной магнитной дыры убивает быстрее, чем гравитационное поле. В той области, где гравитационные силы притяжения равны магнитным силам отталкивания, действующие на нейтроны, может образовываться плотная нейтронная оболочка, в которой бета-распад нейтронов подавлен. Следовательно, массивная магнитная дыра, окруженная плотной нейтронной оболочкой, может считаться разновидностью нейтронной звезды.
Расчет.
Я проделал более детальный анализ своего старого
расчета и нашёл в нем одну ошибку.
Минимальная масса магнитной дыры может быть даже меньше, чем это следовало
из первого расчета. Но определить её точно пока не представляется возможным,
поскольку мы не знаем магнитный момент нуклонного остатка, X-бозона.
Ниже я буду говорить о вложении нуклонов. Мы ставим целью найти массу
и энергию минимально возможной магнитной дыры, способной разрушать нуклоны,
и поглощать нуклонные остатки. Нас в этом подходе будет интересовать поведение
массы и энергия магнитной связи объекта, который мы собираем. Поэтому, говоря
о вложении нуклонов, мы учитываем лишь магнитные взаимодействия нуклонов,
считая их прозрачными, и пренебрегая элементарным зарядом протона. Вложение
нуклонов друг в друга не следует понимать буквально. Расчет приближенный.
Магнитная дыра не состоит из нуклонов. Она захватывает нейтрон, и при этом
выбрасывается антинейтрино; а захватывая протон, выбрасывает позитрон. Грубо
говоря, она состоит из бозонов, нуклонных остатков, квантов магнитного поля.
Магнитный момент нуклонного остатка конечно же отличается от магнитного
момента нуклона. Поэтому наш числовой результат - грубое приближение. Но
у коллайдера LHC - запас приличный. Он может породить частицу массой равной
7000 масс нуклонов.
Предположим, что нуклон представляет собой вакуумный токовый вихрь, который мы представим в виде кольцевого контура, по которому течет ток I, создаваемый движением элементарного заряда по окружности некоторого радиуса R со скоростью света. Тогда в плоскости контура будут существовать магнитное поле, индукция которого в центре витка есть:
B = μ0I / 2R. (1)
Магнитная энергия кольцевого контура:
E = pB. (2)
Где p - магнитный момент нуклона, который можно расписать так:
p = IS = IpR2 .(3)
Преобразуя, получим:
E = μ0pRI2/2, (4)
Поскольку нуклон обладает магнитным полем, то его масса может быть разложена на две части, одна из которых, связана с энергией магнитного поля нуклона, а вторую назовем масса нуклонного остатка, или конденсатной массой:
m = mмагн.поля + mостатка. (5)
Умножая это выражение на c2, мы получим уравнение для энергий.
mc2 = mмагн.поляc2 + mостаткаc2. (6)
С учетом (4) выражение (6) привет вид
mc2 = μ0pRI2/2 + mостаткаc2. (7)
"Вкладываем" два нуклона один в один. Пренебрегаем поляризуемостью и связанным с этим изменением дипольного момента. Поскольку в первом слагаемом ток увеличивается в два раза, а квадрат тока возрастает четыре раза, то энергия магнитного поля динуклона возрастет в 4 раза. В правую сторону уравнения мы также должны добавить энергию излученного фотона, которая будет равна pB=μ0pRI2/2. Его происхождение заключается в следующем. Один нуклон своим магнитным полем подтянул к себе второй нуклон, затратив при этом работу за счет потери своей конденсатной массы. Второй нуклон приобрел кинетическую энергию, которую он потерял слипшись с первым нуклоном. Эта кинетическая энергия превратилась в энергию фотона, которую мы записываем как третье слагаемое в следующем уравнении.
2mc2 = 22 μ0pRI2/2 + mостаткаc2 + μ0pRI2/2. (8)
"Вкладываем" третий нуклон. Энергия магнитного поля три-нуклона возрастет в 9 раз. В правую сторону уравнения мы должны добавить энергию излученного фотона, которая будет равна p·2B. Этот фотон энергичней в два раза первого, поскольку третий нуклон ускорялся полем динуклона.
3mc2 = 32μ0pRI2/2 + mостаткаc2 + μ0pRI2/2 + 2μ0pRI2/2. (9)
"Вкладываем" N-ый нуклон. Энергия магнитного поля N-нуклона возрастет в N2 раз. В правую сторону уравнения мы должны добавить энергию излученного фотона, которая будет равна p(N-1)B. При этом конденсатная масса, mостатка, станет равной нулю.
Nmc2 = N2μ0pRI2/2 + μ0pRI2/2 + 2μ0pRI2/2 + ... + (N-1)μ0pRI2/2. (10)
Преобразуем и получаем:
mc2 / (μ0pRI2/2) = (N2 + 1 + 2 + 3 + ... + (N-1)) / N. (11)
Правая сторона в последней формуле при больших стремится к числу 3N/2. Поэтому мы можем записать
N = (2/3)mc2 / pB. (12)
Проделав несложные преобразования, можно получить:
N = (4/3)(p/pn) / α, (13)
где: pn= qh/(4pm) - ядерный магнетон; α - постоянная тонкой структуры.
Подставляя в формулу 13 значение магнитного момента нуклона, мы получим число N.
Если сборка производится из нейтронов, то N = 350, если из протонов,
то N = 510, если нуклонный остаток имеет ядерный магнетон, то
N = (4/3) / α = 183.
Дальнейшее поглощение нуклонов не может приводить к росту магнитного поля,
поскольку масса остатка будет отрицательной. Следовательно, мы получили
предельное поле, попадая в которое, нуклон сбрасывает позитрон или антинейтрино,
излучает фотон, и, превратившись в бозон, увеличивает радиус магнитной дыры.
Bmax = NB. (14)
Анализируя слагаемые в формуле 10, заключаем что при создании магнитной
дыры
2/3 от энергии покоя нуклонов сборки ушло на создание магнитного поля дыры,
а 1/3 - на излучение.
Энергия связи магнитной дыры соответствует энергии излучения.
Приведем результаты, если магнитный момент нуклонного остатка равен магнитному
моменту протона. В этом случае, энергия столкновения должна соответствовать
510 а.е.м., или 255 а.е.м. на одну частицу в лобовом столкновении. Масса
минимально возможной магнитной дыры, способной поглощать нуклоны, будет
(2/3)·510а.е.м. = 340 а.е.м. Энергия
уносимая излучением и лептонами будет соответствовать массе (1/3)·510а.е.м.
= 170 а.е.м.
Полученный результат для минимальной магнитной дыры дает порядка одной трети
ТэВ.
Это в три раза меньше, чем может дать Теватрон.
Почему она не получена на нем?
Во-первых, мы не знаем магнитный момент нуклонного остатка.
Во-вторых, не исключено, что она может быть рождена в столкновении двух
кварков.
А энергия переносимая каждым кварком на Теватроне тоже порядка 1/3 ТэВ.
В-третьих, на Теватроне сталкивают протон и антипротон, несущие противоположные
электрические заряды, а, значит, магнитная индукция в точке на центре линии,
соединяющей протон и антипротон, движущихся по почти параллельным линиям,
будет равна нулю, B=0. На LHC сталкивают протоны, а значит, магнитная индукция
в точке на центре линии соединяющей протоны, движущихся по почти параллельным
линиям, будет удвоена, B=2B1.
Второй подход. Создание Магнитной Дыры.
11.04.2009 г., переработано 02.02.2010 г.
Второй подход по получению предельного магнитного поля основан на компьютерном моделировании столкновений протонов. Полученный результат совпадает с результатом первого подхода с высокой точностью, а это значительно усиливает степень доверия результату: "Магнитная дыра может быть создана в столкновениях протонов, имеющих энергию 0,25 ТэВ, если магнитный момент захватываемого х-бозона равен магнитному моменту протона".
Что будет с нуклоном, имеющим собственный магнитный момент
p, при попадании в такое магнитное поле B, когда энергия
pB окажется равной энергии покоя нуклона mc2? Для
того, чтобы ответить на этот вопрос рассмотрим аналогию. Что будет с частицей
массы m при её перемещении с бесконечности на такое расстояние
R к массивному объекту массы М, при котором, изменение потенциальной
энергии их взаимодействия GMm/R2 станет равным половине
энергии покоя частицы mc2/2. Приравнивая эти энергии
и сокращая на m, мы может получить форму для радиуса черной дыры.
Следовательно, возвращаясь от гравитационных взаимодействий к магнитным,
заключаем, что равенство pB=mc2 является уравнением, с
помощью которого мы можем вычислить индукцию магнитной дыры. Рассмотрим
еще одну аналогичную формулу, q2/(4pε0R)
= mc2. Это формула, с помощью которой, мы можем определить
классический радиус частицы, обладающей электрическим зарядом. Вокруг неё
существует электрическое поле. Поле имеет энергию, а, соответственно, и
массу. Если мы просуммируем всю массу поля, полагая радиус R равным
нулю, то масса поля будет бесконечной, что абсурдно. Если же мы просуммируем
всю массу поля лишь от бесконечности до радиуса R, равного классическому
радиусу частицы, то она будет равна массе этой частицы. Другими словами,
масса элементарного заряда находится везде за пределами классического радиуса
заряженной частицы, а внутри него ничего нет, - там электрическая дыра.
Электрическая дыра не растет, поскольку электрические заряды одного знака
отталкиваются. Поскольку выражение pB=mc2 подразумевает
не монопольную структуру а дипольную, то препятствия для синтеза этих структур
нет, если протон, испытывая распад, выбросит позитрон, а его остаток, будет
"магнитной таблеткой", х-бозоном.
При столкновении двух протонов, один протон, с магнитным моментом p,
попадает в магнитное поле второго протона, а второй протон попадает в магнитное
поле первого протона. Из этого следует, что мы можем смоделировать программу
и проследить за изменением магнитной энергии pB в сравнении с энергией
покоя ротона mc2. Изменение магнитной энергия в данном
случае подобно изменению потенциальной энергии падающего тела в гравитационном
поле черной дыры. Для падающего тела потенциальная энергия убывает, но возрастает
кинетическая энергия. Падение заканчивается столкновением, при котором,
кинетическая энергию переходит в тепло и излучается в космос, а эту
энергию уже не вернешь, - это уже эквивалент энергии связи бозонного конденсата
магнитной дыры.
Определим величину pB, где p - дипольный магнитный момент одного протона, а B - магнитная индукция, создаваемая вторым протоном. Рассмотрим задачу не в системе координат, связанной с коллайдером, а в системе покоя первого протона. Изменением величины дипольного момента, связанное с изменением магнитной индукции, создаваемой пролетающим рядом протоном, пренебрегаем. Магнитная индукция - величина переменная и во времени, и в разных точках внутри контура первого протона.
B = μ0qvSin(v,r) / (4pr2).
Пускай второй протон пролетает по прямой, лежащей в плоскости контура S первого протона, на расстоянии rmin от контура. Тогда формулу E = pB заменим на следующую:
dE = p (BdS) / S.
Составим программу, а компьютер вычислит и просуммирует все dE, выдавая в результате энергию магнитного поля и отношение этой энергии к энергии покоя протона.
Расстояние rmin по порядку величины сравнимо с расстоянием максимального сближения двух заряженных частиц, когда кинетическая энергия равна потенциальной энергии электрического отталкивания:
Ekin = q2/(4pε0rmin).
Кинетическая энергия при высоких энергиях есть произведение импульса на скорость света: Ekin=Pc.
E2 = m2c4 + P2c2;
E2 = m2c4 + Ekin2;
Ekin = (E2 - m2c4)0.5.
На этом рисунке показана картинка для сравнительно низких скоростей, соответствующих полной энергии налетающей частицы E=1,3mc2.
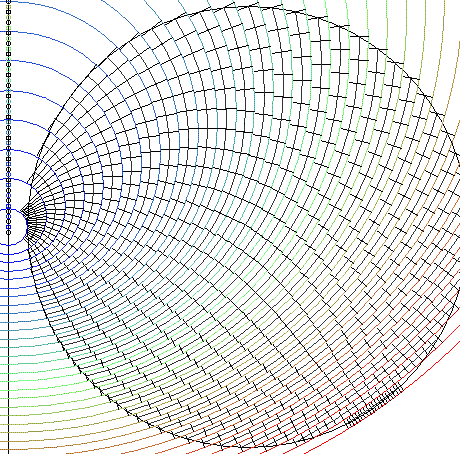
На следующем рисунке показана картинка для умеренных скоростей (v=0,968c), соответствующих полной энергии налетающей частицы E=4mc2.

Следующий рисунок соответствует скорости налетающей частицы (v=0,999999998c) и полной энергии 16000 mc2. В системе координат коллайдера это соответствует примерно 126mc2, или чуть больше 0,1 ТеВ на протон.

Исследование дальнейшего повышения энергии столкновений требует ускорение работы компьютера, или облегчение программы, отключение рисунков и т.п.
14.04.2009 г. Программа частично ускорена и уже выдает результаты.
Таблица результатов по столкновениям протонов для случая с энергией налетающей частицы E = mc2/(α/2)2 = 75115,461mc2, или в системе координат связанной с коллайдером E* ~ mc2/(α/2) = 2·137mc2,
| Слоев \ Делений | 10 | 100 | 1000 | 10000 | 100000 |
| 1000 | 77,011 | 15,354 | 7,2235 | 6,8920 | 6,8895 |
| 10000 | 50,059 | 7,4219 | 1,8272 | 1,2671 | 1,2545 |
| 100000 | 37,304 | 5,1894 | 1,3317 | 0,9589 | здесь |
| 1000000 | 31,027 | 4,6898 | 1,2868 | 0,9353 | очень |
| 10000000 | 29,481 | 4,6410 | 1,2830 | долго | считает |
Колонка "Слоев" означает количество просчитанных и просуммированных слоев, ближайших к пролетающей частице. См. рисунки выше. Колонка "Делений" означает количество "криволинейных прямоугольников" в каждом слое. Замечаем, что при количестве делений, равном 10000, точность расчета уже достаточно удовлетворительна.
В ячейках записано отношение энергии покоя протона mc2 к энергии pB. Результат можно определить по числу в правом нижнем углу таблицы. Если там число больше единицы, то создание капкана на такой энергии столкновений невозможно, если же там число меньше единицы, то капкан возможен. Критическая энергия определится тогда, когда в правом нижнем углу мы увидим число очень близкое к единице.
Проследив за поведением чисел в таблице, приходим к выводу, что магнитный капкан может быть создан на столкновениях протонов с энергиями даже чуть меньше, чем mc2/(α/2) ~ 274mc2. Но первый подход давал нам необходимую суммарную энергию столкновений 2,793(4/3)/α~ 510mc2. Делим это на два, получаем примерно 255,2mc2, или в системе покоя одного из протонов второй протон должен иметь энергию примерно 65107mc2. Проверим этот вариант на компьютере, будет ли он близок к единице?
| Слоев \ Делений | 10 | 100 | 1000 | 10000 | 100000 | 1000000 |
| 1000 | 77,013 | 15,359 | 7,2355 | 6,9043 | 6,90170 | 6,90167 |
| 10000 | 50,068 | 7,4397 | 1,8689 | 1,3292 | 1,31767 | 1,31755 |
| 100000 | 37,351 | 5,2482 | 1,3912 | 1,0269 | 1,0191 | |
| 1000000 | 31,237 | 4,7849 | 1,3486 | 1,0034 | ||
| 10000000 | 29,850 | 4,7418 | 1,3451 | ~ 1 | ||
| 100000000 | 29,808 | 4,7408 | ~ 1 |
Итак, результат второго подхода идеально совпадает с результатом первого подхода. Подходы совершенно независимы и основаны на разных исходных идеях: там - оценка минимальной энергии капкана на основе "вложений" нуклонных токовых контуров друг в друга; здесь - оценка минимальной энергии столкновений, при которой один протон попадают в капкан второго протона. Идеальное совпадение результатов говорит о том, что предположение о возможности создания магнитного капкана на коллайдерах слишком высока. Глобальная катастрофа может произойти при энергиях сталкивающихся протонов порядка 0,25 ТэВ на протон.
3 февраля 2010 года.
Несмотря на то, что 20-го ноября был подан иск в Европейский Суд по Правам Человека, 23-но ноября 2009-го года ЦЕРН начал осуществлять столкновения на Большом Адронном Коллайдере. До 16 декабря было осуществлено порядка миллиона столкновений с энергиями 0,45 ТэВ на протон, и порядка нескольких десятков тысяч столкновений с энергиями 1,18 ТэВ на протон. 16 декабря Коллайдер был остановлен. Новые столкновения с энергиями 3,5 ТэВ на протон запланированы на 20-е февраля.
Можно ли считать, что столкновения на энергиях ниже 1,18 ТэВ уже не опасны?
Нет!
Во-первых, осуществите порядка миллиарда столкновений. Если не взорвемся, значит эти энергии безопасны с большой долей вероятности.
Во-вторых, скорость роста магнитной дыры до полного уничтожения Земли не может быть вычислена точно. Перебирая разумные оценки скоростей захвата вещества магнитной дырой, заключаем, что магнитной дыре на полное уничтожение Земли требуется от 1000 секунд до 1000 дней. Поскольку тысяча дней еще не прошла, мы не можем сказать, что магнитная дыра не была создана в декабре 2009-го года.
Если магнитный момент х-бозона равен магнитному моменту протона, то магнитная дыра может быть создана в столкновениях 0,25 ТэВ на протон. Если магнитный момент другой, то и требуемая энергия столкновения будет другой.
Третий подход.
Характеристики магнитной дыры.
Этот пункт создан в период 16-25 апреля 2009. Впоследствии замечено, что здесь требуется перейти от квантования по магнитному потоку к квантованию по энергиям. Предварительный анализ показывает, что основные выводы при этом не изменятся.
Индексами 1, n, pr обозначены величины, относящиеся к минимальной магнитной дыре; произвольной магнитной дыре; и протону, соответственно.
Предположим, что магнитный поток пронизывающий магнитную дыру квантован. Тогда, если предположить, что в физическом вакууме существует предельное магнитное поле, и это поле является константой в плоскости круга магнитной дыры, то радиусы и площади магнитной дыры могут принимать только серии определенных значений.
Пускай минимальная магнитная дыра радиуса R1, имеющая площадь S1 и толщину d1, пронизывается предельным магнитным полем B1. Произведение B1S1 равно одному кванту магнитного потока Φ1. Удвоенному кванту магнитного потока соответствуют величины R2, S2, d2, B2. Ниже мы убедимся, что предельное магнитное поле не зависит от радиуса, а радиус и толщина магнитной дыры растут пропорционально.
В каждой точке в плоскости минимальной магнитной дыры существует предельный токовый вихрь, создаваемый виртуальными электрон-позитронными парами. Для произведения расчетов мы заменяем предельный токовый вихрь виртуальных пар на эквивалентный ток, создаваемый элементарными зарядами, движущимися по окружности радиуса R1 со скоростью света. Количество этих воображаемых элементарных зарядов обозначим буквой N1.
Тогда выражение для тока будет иметь вид:
I1 = N1q / t = N1q
/ (2pR1 / c) = N1qc / 2pR1.
In = Nnqc / 2pRn.
Применяя известные формулы Φ1 = B1S1; Φn = nh / 2q; B1 = μ0I1 / 2R1; c2 =1 / μ0ε0; q2 = 2αhcε0, находим число N.
N1 = 1 / α
~ 137,036.
Nn = n / α ~ n·137,036.
В правильности полученных формул можно убедиться, отправив по окружности 137,036 элементарных зарядов со скоростью света. Каждый из этих зарядов создает в центре витка индукцию B = μ0qc / 4pR2. Умножив это выражение на 1/α и на площадь круга, pR2, получим квант магнитного потока, Φ1 = μ0qc / 4α = h / 2q.
Предположим, что протон, попадая в магнитное поле B, распадается и его бозонный остаток конденсируется на магнитную дыру. Предположим, что распад протона произойдет тогда, когда энергия магнитного взаимодействия поля дыры B, с током в протоне Ipr, или с магнитным моментом протона станет равной энергии покоя протона, умноженной на некоторое число x. Мы проанализируем несколько вариантов на роль числа x, записывая формулы друг за другом, но окрашивая их в разные цвета. Черным цветом - общая формула для квантового числа n=1; красным - интересная резонансная; зеленым - х переброшен справа налево - к ядерному магнетону; синим цветом х спрятан в магнитной аномалии протона; черным - общая формула для произвольного n.
B1IprSpr = xmc2.
B1IprSpr =2p2mc2.
B12pn
=mc2.
B1ppr =mc2.
BnIprSpr = xmc2.
Здесь: B1 = μ0I1 / 2R1 - индукция дыры; I1 = qc / 2pαR1 - ток воображаемых зарядов дыры; Ipr = qc / 2pRpr - ток элементарного заряда в протоне; Spr = pRpr2 - комптоновская площадь протона; Rpr = h / 2pmprc - комптоновский радиус протона. В формуле B12pn =mc2 величина 2pn есть предполагаемый магнитный момент остатка распавшегося протона, имеющий спин, равный единице, чем и объясняется возникновение двойки перед ядерным магнетоном pn. Формула B1ppr =mc2, содержащая аномальный магнитный момент протона, ppr =2.7928pn, может быть преобразована к виду B1IprSpr = xmc2, где x = 1/2.7928.
Применив приведенные выше формулы, мы можем получить некоторые характеристики магнитной дыры. Результаты будут выглядеть красивее при введении замены y=(2x)0.5 и наряду с использованием комптоновской радиуса протона Rpr, использовать комптоновскую длину протона λpr = 2pRpr.
R1 = Rpr / y.
R1 = Rpr / 2p.
R1 = Rpr = 2,103089·10-16
м.
R1 = Rpr / 0,846
= 2,485228·10-16 м.
Rn = n0.5Rpr / y.
Ток:
I1 = yqc / αλpr.
I1 = qc /
αRpr.
I1 = qc /
αλpr = 4981134 A.
I1 = 0,846qc /
αλpr. = 4215214 A.
In = yn0.5qc / αλpr
Магнитная индукция:
B1 = y2μ0qc
/ 4pαRpr2.
B1 = μ0pqc
/ αRpr2.
B1 =
μ0qc / 4pαRpr2
= 1,488162623·1016
Тл.
B1 = 0,8462μ0qc
/ 4pαRpr2
= 1,06569564·1016
Тл.
Bn = y2μ0qc
/ 4pαRpr2.
Первый вывод: Магнитная индукция в последней формуле не зависит от n, следовательно, магнитная индукция одинакова для магнитного капкана любого размера. Поскольку, выше получены зависимости Rn ~ n0.5 и In ~ n0.5 то ток должен расти пропорционально радиусу. Это в свою очередь указывает нам на кажущееся противоречие, ведь мы предположили, что этот ток воображаемый, и является обычной заменой предельного токового вихря виртуальных частиц в плоскости дыры, на эквивалентный ток по кольцевой окружности. Тогда, какой же он предельный, если зависит от радиуса? Ниже это противоречие снимается тем, что толщина дыры растет пропорционально радиусу.
Магнитный момент магнитной дыры получим с учетом того, что собственный магнитный момент элементарных частиц превосходит орбитальный момент в два раза, а также в предположении, что спин виртуальных пар равен единице. Тогда классическое выражение p = IS, приобретет дополнительный множитель - двойку.
p1 = 2I1S1 = Rprqc
/ yα
p1 = Rprqc / 2αp
p1 = Rprqc /
α = 1,384278304·10-24
Дж/Тл.
p1 = Rprqc /
0,846α
= 1,6358068·10-24
Дж/Тл.
pn = Rprn1.5qc / yα
Вычислим энергию магнитной дыры.
E1 = p1B1 = yhc
/ αλpr
E1 = p1B1 =
hc
/ αRpr
E1 = p1B1
= hc /
αλpr = 2,060031232·10-8
Дж, или 137.036mc2.
E1 = p1B1
= 0,846hc /
αλpr = 1,47521935·10-8
Дж.
En = pnBn = yhcn1.5 /
αλpr
Индуктивность минимального магнитного капкана можно получить, приравнивая энергию контура с током LI2/2 энергии E.
L1 = λpr
μ0 / y
L1 =
Rpr
μ0
L1 =
λpr
μ0 = 1,660532598·10-21
Гн.
L1 = λpr
μ0 /
0,846
= 1,962257543·10-21 Гн.
Ln = λprμ0n0.5
/ y
Электроемкость магнитного капкана получим приравнивая энергию заряженного конденсатора Q2 / 2C энергии E. При этом заряд Qn равен числу элементарных зарядов q, Qn=nq/α.
C1 =
λprε0
/ y
.
C1 =
Rprε0.
C1 =
λprε0
= 1,17000110·10-26 Ф.
C1 = λprε0
/ 0,846
= 1,38259465·10-26
Ф.
Cn = λprε0n0.5
/ y
Второй вывод: Ошеломляющая простота формул для индуктивности и емкости магнитного капкана подтверждает его реальность.
Предельное напряжение получим, пользуясь определением электроемкости C=Q/U.
U1 = qy / αλprε0.
U1 =
q / αRprε0.
U1 =
q / αλprε0
= 1876544054 В.
U1 =
0,846q / αλprε0.
= 1343821425
В.
Un = n0.5yq / αλprε0
Период собственных колебаний.
T1 =2p(L1C1)0.5
= 4p2Rpr/
yc.
T1 =2p(L1C1)0.5
= λpr
/ c. Это равно комптоновскому периоду протона.
T1 =2p(L1C1)0.5
= 4p2Rpr
/ c = 2,7694703·10-23
c.
T1 =2p(L1C1)0.5
= 4p2Rpr
/ 0,846c = 3,2726933·10-23
c.
Tn = 2p(LnCn)0.5
= 4n0.5p2Rpr
/ yc.
Комптоновский период магнитной дыры.
T1c = h / E1
= αλpr / yc
T1c =h / E1 =
αRpr
/ c.
T1c = h / E1 =
αλpr
/ c.
T1c = h / E1 = αλpr
/ 0,846c
Tnc = h / En = αλpr
/ ycn1.5.
Волновое сопротивление получим, разделив предельное напряжение на ток.
Z1 = U1 / I1 = Z0
Zn = Un / In = Z0
Величина Z0 =(μ0/ε0)0.5 есть волновое сопротивление физического вакуума. Но магнитный капкан не является волной, распространяющейся в каком-то конкретном направлении со скоростью света. Капкан это токовый вихрь, созданный в вакууме из виртуальных частиц. С капканом можно связать покоящуюся систему координат.
Используя формулу для полного сопротивления, z = (R2 +(XL -XC)2)0.5, можно убедиться что полное сопротивление магнитного капкана равно нулю, если активное сопротивление R равно нулю. А оно действительно будет равно нулю, поскольку ток в контуре создается синхронным движением виртуальных частиц. Активное сопротивление появится в том случае, если в капкан попадут другие частицы - центры рассеяния энергии. Но при этом другие частицы распадаются в предельном поле капкана, подпитывая его своей энергией, и, превращая капкан в растущую автоколебательную систему.
Подставляя наши разные L, C, T в формулы XL= ωL= 2pL/T, XC = 1 / ωC = T / 2pC, z = (R2 +(XL -XC)2)0.5, убедимся что они дают одинаковые результаты:
XL1= XL1
= XL1 = XL1
= XLn = μ0c
= (μ0/ε0)0.5
= Z0
XC1 = XC1 =
XC1 = XC1
= XCn= 1 / cε0
= (μ0/ε0)0.5
= Z0
z1 = z1 =
z1 = z1
= 0.
Итак, магнитная дыра обладает индуктивностью, емкостью, собственными незатухающими колебаниями. Развивая аналогию дальше, мы можем вообразить её в виде консервной банки, боковая поверхность которой является одновитковой катушкой, и нижняя и верхняя крышка - обкладками конденсатора. Внутри банки существуют предельные токовые вихри виртуальных электрон-позитронных пар, которые мы мысленно перенесли на боковую поверхность в виде тока воображаемых элементарных зарядов.
Используя формулы для емкости плоского конденсатора, C = ε0εS/d, и для индуктивности одновитковой (N=1) катушки, L = μ0μN2S/d, и, сравнивая их с нашими формулами Cn = λprε0n0.5/y, Ln = λprμ0n0.5/y, Sn = pRn2, Rn = n0.5Rpr/y, убеждаемся, что толщина магнитной дыры ровно в два раза меньше её радиуса.
dn = Rn / 2.
Анализ результатов.
Итак, что же представляет собой магнитная дыра?
С учетом результатов, полученных в этом разделе, она может
представлять собой один из четырех объектов:
1. Постоянный магнит, создаваемый током In = yn0.5qc
/ αλpr , текущим
по контуру индуктивностью Ln =
λprμ0n0.5
/ y;
2. Постоянный магнит, создаваемый постоянным током I = In,
текущим по контуру индуктивностью L = Ln /2
; и одновременно электрический диполь, характеризуемый постоянным
напряжением U = Un , возникающим между обкладками конденсатора
емкостью C = Cn/2.
3. Колебательный контур, с переменным током, амплитудное значение которого,
есть I~ = In, текущим по контуру индуктивностью
L = Ln; и переменным напряжением U~
= Un, возникающим между обкладками конденсатора емкостью
C = Cn.
4. Контур, создающий постоянное магнитное поле, поддерживаемое постоянным
током Ic. В этом контуре могут возникать электромагнитные
колебания с амплитудным значением тока I~. При этом
Ic и I~ могут быть произвольными,
но Ic + I~ = In и
каждый из них не больше In. L = Ln;
C = Cn.
В пункте 2 мы разделили вычисленные индуктивность и емкость на два, поскольку в этом случае логично предположить, что энергия такой магнитной дыры E распадается на две равные части LI2/2 и CU2/2, не меняющиеся во времени. В пунктах 3 и 4 деления на два нет, поскольку там осуществляются колебания и происходит перекачка энергии из магнитного поля в электрическое и наоборот.
Наиболее реалистичными являются первый и четвертый вариант. Второй вариант возможен в том случае, если виртуальные электроны и позитроны в постоянном магнитном поле смещаются друг от друга в направлении силовых линий магнитного поля.
Если осуществляется третий или четвертый вариант, то магнитная дыра есть контур, в котором осуществляются электромагнитные колебания. Эти колебания будут незатухающими, если вокруг такой дыры нет вещества. Если вещество есть, то оно может привести к рассеянию энергии дыры, либо быть поглощенным дырой, подпитывая её и увеличивая дыру. Рассеяние энергии дыры могло бы происходить, если бы вещество находилось сравнительно далеко от дыры, то есть, в слабом магнитном поле. Но магнитное поле малой дыры чрезвычайно высокочастотно (1022Гц), а поглощение кванта такой частоты равносильно поглощению дыры, что невозможно. Поглощение вещества дырой может происходить в том случае, если оно находится достаточно близко к дыре, то есть, в её сильном магнитном поле. Если дыра растет, то частота её собственных колебаний падает, а это приведет к возможности рассеяния энергии дыры на окружающем её веществе, когда дыра станет достаточно большой.
Энергия магнитной дыры растет пропорционально кубу её радиуса. Период колебаний растет пропорционально радиусу. Частота есть величина обратная периоду. Оценочный расчет показывает, что магнитная дыра, образованная в случае поглощения Земли будет иметь собственную частоту порядка 1 МГц; при поглощении Солнца - 10 кГц; при поглощении звезды в сотню солнечных масс - 1 кГц. С учетом гравитационных поправок эти частоты могут быть значительно увеличены за счет гравитационного красного смещения. Это значит, что наблюдаемые частоты пульсаров (до 0.7 кГц) свидетельствуют о том, что пульсары на самом деле могут быть магнитными дырами, либо содержать магнитные дыры в своих центрах, сдерживая нейтронную оболочку от коллапса своим мощным магнитным полем.
Однако, для объектов с массой порядка сотых долей массы Солнца, радиус магнитной дыры становится меньше гравитационного радиуса. Но для того, чтобы судить о гравитационном радиусе, мы должны знать, а чему равна гравитационная масса магнитной дыры? То, что у неё есть инертная масса, не вызывает сомнений. Но равна ли гравитационная масса инертной массе в этом случае? И является ли гравитационное поле магнитной дыры изотропным, или же оно имеет осе-симметричную диаграмму направленности?
Оценочный радиус магнитной дыры при поглощении
Земли ~ 6 метров;
Солнца ~ 400 метров;
звезды в 100 масс Солнца ~ 2 км.
В случае Солнца и звезд это меньше соответствующего Шварцшильдовского радиуса. Но с учетом сказанного выше по поводу гравитационной массы, - вполне реально.
Мы начали из квантованного магнитного потока. Для того, чтобы магнитный поток возрос на единицу, магнитная дыра должна поглотить одновременно пачку нуклонов. Одновременное поглощение "пачки нуклонов" звучит коряво. Но, во-первых, а почему бы и не поглощать пачками. Во-вторых, квантование магнитного потока сейчас может быть отброшено, - оно было необходимо лишь как каркас, с помощью, которого мы производим вычисления. В-третьих, возможно, что магнитная дыра может принимать любые значения квантового числа n, в том числе и дробные, но целые числа при этом становятся резонансными числами, к которым стремится магнитная дыра, - таких резонансов, к которым стремятся планеты в Солнечной системе, большое множество.
Что такое "Большой Взрыв" и кто такие бигбангеры?
Большой Взрыв это космологическая модель эволюции Вселенной. Согласно этой гипотезе Вселенная родилась из ничего 10-20 млрд. лет. В течение последних 10 лет этот возраст значительно уточнен и сейчас Вселенной отводят порядка 13 млрд. лет от роду. Гипотеза Большого Взрыва поддерживается религией, а теория БВ превратилась в догму. Наиболее одиозные сторонники этой теории сейчас её считают не теорией, а фактом.
Теории БВ противостоят множество стационарных моделей Вселенной. Согласно стационарным моделям[3] Вселенная вечна и не эволюционирует. Но её составляющие: галактики, звезды, планеты, цивилизации эволюционируют, рождаются, живут, умирают.
Сторонники БВ сейчас хотят посмотреть на первые микросекунды рождения Вселенной. Для этого они планируют сталкивать пачки протонов к колоссальными энергиями на коллайдерах.
Этим они не докажут свою ущербную теорию, но с большой степенью вероятности могут инициировать образование микроскопических магнитных дыр, а это в последствии приведет к взрыву Земли, а затем и Солнца. Вот этот взрыв и будет натуральным Большим Взрывом. Дальнейшее распространение магнитной дыры очень маловероятно и скорее всего она распадется. Хотя не исключено, что магнитные дыры скапливаются в центрах галактик. Только в нашей галактике мы наблюдаем сотни взрывов звезд в год. Вполне возможно, что так заканчивают свой путь цивилизации, что приводит к их размножению.
В связи со сказанным, сторонники гипотезы БВ уже не могут считаться безобидными сторонниками теории Вселенского Большого Взрыва, но прямыми исполнителями Земного Большого Взрыва.
... по поводу космических частиц.
Вот сравнение:
ТэВ-нейтрон разрушает ядро.
Медленный нейтрон поглощается ядром.
Космически порожденная магнитная петля разрушается из-за
того что имеет релятивистскую скорость.
Коллайдерно порожденная магнитная петля движется медленно
и может захватывать вещество Земли и уничтожить всех нас.
Вред гипотезы БВ
Гипотеза БВ вредна поскольку ради её спасения придуманы костыли в виде темной энергии и темной материи. Согласно гипотезе БВ во Вселенной нормальной материи всего лишь несколько процентов, но зато темной энергии более 70%. Попросту говоря, темная энергия это энергия пространства, вакуума. Бигбангеры считают, что вакуум "железный" аж до планковских размеров. Но если посмотреть на решеточную модель в настоящей работе, то мы увидим, что пределы существуют значительно ближе. В нашей решетке одновременно не существуют линии ближе комптоновского радиуса протона (с точностью до числового коэффициента). Но если взять временную развертку, то пространство между этими линиями, заполняется звеньями квази-замкнутой окружности. Длина оного звена с точностью до числового коэффициента равна планковской длине, и живет это звено лишь в течении планковского времени. Звено сменяется другим звеном, образуя минимальный угол в пространстве-времени. Поворот в пространстве-времени означает изменение скорости. Пространство-время в нашей модели на двадцать порядков нежнее, чем "железное" пространство в стандартной модели. Наше главное квантовое число, описывающее пространственно-временную решетку N=3*1020. В стандартных моделях описывается вакуумная пена на планковских масштабах, т.е, у них Nst=1040.
Наша модель указывает на возможность существования значительно меньшего критического магнитного поля. В нашей модели возможность глобальной катастрофы предугадывается легче. Бигбангеры яростно отсекают любую модель, которая противоречит их религии, обвиняя сторонников стационарных моделей в некомпетентности. Тем самым они приближают нас к глобальной катастрофе.
Фальсификации бигбангеров.
Сторонники теории БВ утверждают о том, что якобы они что-то там предсказывали и их предсказания сбылись.
Но вот факты:
Сторонники статичной модели предсказали фоновое излучение за 50 лет до
Гамова. Их предсказания значительно точнее.
Предсказания фонового излучения[1]:
Guillaume: 5-6 K, опубликовано в 1896.
Eddington: 3.18 K, опубликовано в 1926.
..
Бигбангер Гамов: Т = 7 К в 1953; Т = 50 К в 1961,
..
Регистрация фонового излучения:
Regener измерял косвенным методом и получил: 2.8 K в 1933г.
Пензиас и Вильсон: 3.5 ± 1.0 K в 1965г.
Но результат Regener-а "не катит", потому что он основан на статичной/стационарной
модели. Поэтому мы этой фамилии не знаем.
Сравните точность предсказаний и измерений, и сравните с современными измерениями
температуры РФ:
Что такое БВ? Гипотеза, теория или факт?
Об укоренении теории/гипотезы/факта Большого Взрыва в сознании научного сообщества можно почитать в статье Игоря Иванова «Анатомия одной новости, или Как на самом деле физики изучают элементарные частицы»[2].
… Небольшого комментария заслуживает только фраза «... после так называемого
«Большого взрыва», с которого, как предполагают ученые...».
Я понимаю, что этот пассаж покажется журналисту вполне невинным, даже в
какой-то мере «честным», отражающим беспристрастность журналиста — «я лишь
передаю мнение ученых». Пикантность этой ситуации состоит в том, что совсем
недавно, в феврале 2006 года, в NASA разразился административно-политический
скандал, как раз связанный со статусом факта / теории / гипотезы Большого
взрыва.
Суть, вкратце, такова. В октябре 2005 года администрация Джорджа Буша назначила
человека из своего окружения — некоего Джорджа Дойча (George Deutsch), 24-летнего
молодого человека с неоконченным журналистским образованием — специалистом
NASA по связям с общественностью. Его первыми шагами стала попытка заменить
во всей публичной информации NASA все слова «Большой взрыв» на слова «теория
Большого взрыва». Мотивация состояла в том, что Большой взрыв — это не факт,
это мнение ученых, а значит, необходимо постоянно подчеркивать, что это
есть только мнение. Более того, Дойч утверждает, что вопрос о происхождении
мира не столько научный, сколько религиозный, а значит, нельзя подрастающему
молодому поколению говорить о Большом взрыве как факте.
Реакция сотрудников NASA и научного сообщества в целом была бурной, и в
течение нескольких дней Дойч уволился. Подробности этого скандала можно
узнать, например, в блоге CosmicVariance или Bad Astronomy. Суть же можно
сформулировать так: есть вещи, серьезное сомнение в которых эквивалентно
шагу обратно в средневековье. Звезды — вовсе не дырки в хрустальном небосводе;
вся материя действительно состоит из атомов; эволюция Вселенной действительно
началась со сверхплотной и сверхгорячей фазы много миллиардов лет назад.
Всем этим — формально — гипотезам есть столько объективных подтверждений,
что их необходимо считать фактами, несмотря на то, что вы никогда не долетите
до звезд, не пощупаете руками отдельные атомы и не сможете обратить время
вспять (вот, например, подробный список наблюдательных данных, подтверждающих
теорию Большого взрыва). Серьезное обсуждение в популярной литературе возможности,
что это всё неверно, приведет к прямому вреду для молодежи.
Вот так! Подвергать сомнению гипоте.. факт БВ, значит наносить вред молодежи...
Печально...
Будем проверять на коллайдере?
Что верно?
Факт БВ, случившегося 13 млрд. лет назад, или гипотеза Большого Взрыва Земли, который хотят осуществить бигбангеры на коллайдере?
1.
2.
3. Стационарные Модели Вселенной и их Авторы.