THE EARTH'S CORE IS OVERHEATED EMPTINESS

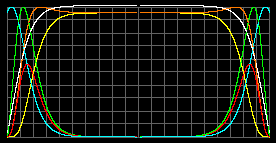
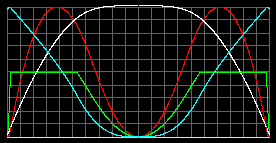
The Sun-like object, M = 1M_Sun; R = 1R_Sun; m_particle = 1.5 a.u.m.

Our model	Standard model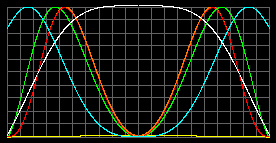
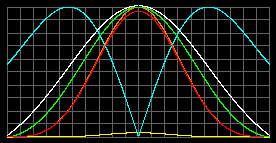
Tcenter = 7.66 millions K. Total pressure pmax =8.4*108atm at r=0.56R Density rmax=2.5 t/m3 at r=0.632R	Tmax=18 millions K. pmax =7.96*109atm at center. rmax=7.8t/m3

Green - concentration of particles; red - gas pressure; yellow - radiation pressure; orange - total pressure; white - temperature; blue - acceleration g. Graphs were normalized to the scale of window and surface gravity acceleration in both cases are equal.

---

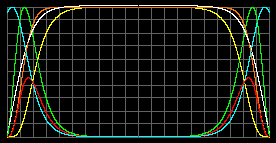
Object with M = 10M_Sun; R = 50R_Sun; m_particle = 1.5 a.u.m.

Our model	Standard model ruined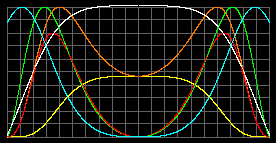
Tcenter = 1.2 millions K. pmax =1.2*104atm at r=0,6R. rmax=0,19 kg/m3 at r=0,717R	Tmax=1.77 millions K. pmax =31519atm at center. rmax=0,2kg/m3 at r=0,617R

As we can see the radiation had naked the center in both cases. The pressure and particles concentration is not sufficient for nuclear fusion in such stars. Mainstream astrophysicists slander us. Or try to hide the radiation pressure under their carpets.

---

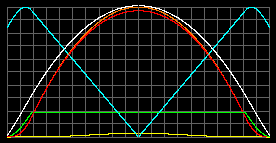
Object with M = 70M_Sun; R = 500R_Sun; m_particle = 1.5 a.u.m.

Our model	Standard model become as ours
Tcenter = 363 thousands K. pmax =45atm at r=0.74R. rmax=1.86 g/m^3 at r=0.88R.	Tcenter = 391 thousands K. pmax = 58atm at center. rmax=1.81 g/m3 at r=0,87R.

Pay attention at the values. Nuclear reactions are impossible for giant stars.

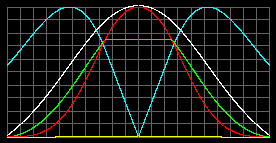
Let's diminish the radius, for example at ten times (object with M = 70M_Sun; R = 50R_Sun; m_particle=1.5 a.u.m.). We'll have almost the same graphs but the temperature will rise ten times, common pressure will rise in 10⁴ times, because it now dependent mostly of radiation. And the density will rise in 10³ times. That is also insufficient. Energy sources of standard astronomy disappeared.

But we have no need to take that to heart. We know the other sources of star's energy. And we need to know the real non-falsified internal structure of stars. Let’s now look at the objects, smaller then our Sun.

---

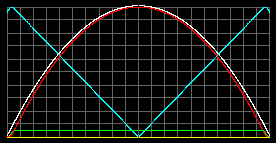
White dwarf, Object with M = 1M_Sun; R = 0.01R_Sun; m_particle = 2a.u.m. Density of condensation of gas into liquid (degenerated gas) = 2*10⁹ kg/m³.

Tcenter = 920 millions K. pmax = 6.9*1016atm r=0,581R. The liquid state with rmax=2*109 kg/m3 stretches from 0.83R to 0.52R.	Tcenter = 1249 millions K. pmax =2.1*1017atm at center. The liquid state with rmax=2*109 kg/m3 stretches from r=0,81R to center.

Pay attention on the temperatures! But this is not so extraordinary if we mention that surface temperatures of some white dwarfs are 10000 K, 60000 K, and higher. (The difference in heights of green graphs is the result of program normalization. In fact we have launched the same density of condensation of gas into liquid.)

---

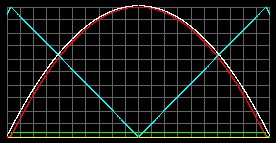
Jupiter-like object: M=0.00095M_Sun; R = 0.1025R_Sun;
m_particle = 4a.u.m. - was taken arbitrarily.

Let's take arbitrarily the density of condensation of gas into liquid equal to 2000 kg/m³ for our equations, and 6000 kg/m³ for standard model.

Tcenter = 183 thousands K. pmax = 6.4*106atm at r=0.57R. The liquid state with rmax=2000 kg/m3 stretches from 0.76R to 0.54R.	Tcenter = 444 thousands K. pmax = 6.4*107atm at center. The liquid state with rmax=6000 kg/m3 stretches from 0.25R to center.

 

---

The Earth-like object: M = M_Earth; R = R_Earth; m_particle = 20a.u.m. - was taken arbitrarily.

Tcenter = 25 thousands K. pmax = 6.6*105atm at r=0.62R. The liquid/solid state with rmax=6000 kg/m3 stretches from 0.97R to 0.47R.	Tcenter = 33 thousands K. pmax = 1.9*106atm at center. The liquid/solid state with rmax=6000 kg/m3 stretches from 0.95R to center.

The difference in heights of green graphs is the result of program normalization. In fact we have launched the same density of condensation of gas into liquid/solid, r=6000 kg/m³.

The received values of temperature surpass the values, proposed in literature, somewhere about 5 times. The central temperature can be decreased by decreasing of the coefficient of temperature gradient. In all upper cases we have used the coefficient 2/5, which is reasonable for gaseous medium, but is controversial for liquid/solid medium. Let's diminish it to 1/10 and try again.

Tcenter = 7.9 thousands K. pmax = 7*105atm at r=0.59R. The liquid/solid state with rmax=6000 kg/m3 stretches from 0.97R to 0.17R.	Tcenter = 8.2 thousands K. pmax = 1.9*106atm at center. The liquid/solid state with rmax=6000 kg/m3 stretches from 0.97R to center.

Let's analyze the graphs in our model. The drop of pressure begins approximately at r=0.6R, but the temperature is already quite high there. That means that there must exist the point of transition of substance from solid state into liquid. It is known from seismology that the border between the core and mantle is situated at r=0.54R. That border strongly reflects P and S waves and refracts the P-waves. Our graphs of pressure and temperature allow us to divide the horizontal graph of density on two regions: solid and liquid. But standard model graphs do not obey us to do that, - the continuing growth of pressure rises the temperature of melting. At last, lets analyze the point of transition from liquid state into gas. It is the boundary between the external and internal core. Standard geology says that external core is liquid and internal core is solid. We say: the external core is liquid; the internal core is gaseous. We can see there the crack at the density graph. But it is known from the thermodynamics that at high temperature there is no distinct boundary between liquid and gas. There must be a smooth transition. Consequently, I'll paint by hand the region of liquid phase in dark-blue color. I'll smooth the crack and paint the gas phase into yellow color.

The external core (dark-blue) is liquid and keeps the S-waves out; the internal core (yellow) is gaseous and keeps both waves out.

Used equations.

If we do not account the light's pressure and mass the following systems is valid.

With Arc Effect.	Standard-like equations.
dp/dr = - gr + 2p/r. dT/dr = - (2/5)mg/k. dM/dr = 4pr2r. g = GM/r2. p=nkT. r=nm.	dp/dr = - gr. dT/dr = - (2/5)mg/k. dM/dr = 4pr2r. g = GM/r2. p=nkT. r=nm.

---

If we account the light's pressure and mass the following systems is valid.

With Arc Effect.	Standard-like equations.
d(p+p')/dr = - g(r+r')+2p/r. dT/dr = - (2/5)mg/k. dM/dr = 4pr2(r+r'). g = GM/r2. p=nkT. r=nm. r'=u/c2. u=3p'. u= 4sT4/c.	d(p+p')/dr = - g(r+r'). dT/dr = - (2/5)mg/k. dM/dr = 4pr2(r+r'). g = GM/r2. p=nkT. r=nm. r'=u/c2. u=3p'. u= 4sT4/c.

If we take into account the density of condensation of gas into liquid/solid, the p=nkT or n=p/(kT) is changed into:

n = p/(kT)	if p/(kT) smaller than nmax.
n = nmax.	if p/(kT) biger than nmax.

---

The temperature gradient equation.

In the case of Earth we tried two variants for temperature gradient:
dT/dr = - (2/5)mg/k and dT/dr = - (1/10)mg/k.
In fact this equation is approximate, - it does not contain the radiation part. The computer modeling had showed me that inclusion of radiative part into the temperature gradient equation almost does not change the graphs. From my point of view the coefficient 2/5 is valid for the ideal gas object in thermodynamical equilibrium. I would name the equation dT/dr = - (2/5)mg/k as the equation of gravitational temperature gradient. This gradient is intrinsic and does not lead to heat transfer from hotter region to cooler region. The heat transfer will begin in the case dT/dr = - ((2/5)+a)mg/k, where a is a coefficient of temperature gradient, responsible for heat transfer, and which value is determined by the thermal conductivity of the gas. I would name the last equation as the equation of total temperature gradient. The computer modeling had showed me that decreasing of the coefficient 2/5 leads to inclination of graphs to the center of the object, but the increasing of the coefficient leads to inclination of graphs out from the center. If the coefficient becomes very small or equal to zero, the system can not be integrated. But when we launch the condensation with some arbitrary n_max, the system becomes integrable again. The cause is clear, - the condensation closes the exponential precipice, appearing at the center of the object in the isothermal case.

The pressure gradient equation.

I saw two types of equation of hydrostatic equilibrium.

dp/dr = - gr, for ideal gas object.
d(p+p')/dr = - g(r+r'), for ideal gas object filled with radiation.

From my point of view these equations lead to errors because they do not account the Arc Effect. These equations are correct for the object filled with non-colliding particles, for example, for star congestions filled be stars, for photon gas enclosed in some vessel, for very rarefied gaseous object with particles having the length of free pass, greater than the object's radius.

If we account the collisions between particles, we'll have the following equations:

dp/dr = - gr + 2p/r, for ideal gas object.
dp/dr = - gr + 2(p-p₀)/r, for ideal gas object, enclosed by the shell with pressure p₀.
d(p+p')/dr = - g(r+r') + 2p/r, for ideal gas object filled with radiation.
d(p+p')/dr = - g(r+r') + 2(p-p₀)/r, for ideal gas object filled with radiation, enclosed by the shell with pressure p₀.

Pay attention that the last item in these equations does not contain the radiative part of pressure, p'. The cause is clear, - the light does not obey the Arc Effect, because the light beam do not change the direction of another light beam at their cross-point; the photons can exert pressure upon matter screen, but photons do not exert pressure upon other photons.

The computer modeling had showed me, that the usage of the symmetrical equation, containing p' in the last item, leads to appearing of a hole in the center of the object. The more the temperature of the object is the more the hole.

March, 2007.

---

Text from May 2000.

Notes from March 2007 I'll paint in yellow.

Any massive object: the Sun, the Earth, a star, a planet, a nuclei of galaxies and quasars are empty inside. This emptiness is filled with rarefied gas and radiation at high temperatures. In average, at constant radius, the more massive object is, the more temperature is inside of its depths...(cut). On the other hand, the further a star on a scale of evolution, is the thinner its shell. The rupture of a star shell leads to the explosion of nova or supernova. (...) To understand these paradoxical conclusions let's try to analyze the dependence of a pressure from the distance to the center of an object.

Let’s assume at first, that the massive object is a giant gas ball. (...) Let’s break a star into a series of concentric layers. The gravity force pulls each layer to the center of the object; and its weight dP is transferred to a bottom layer. Having divided the weight by the area of sphere between these spherical layers we shall receive an increment of a pressure, which is added to the whole pressure, transmitted from the top layer to bottom: dp = dP / S. In order that the object be in balance it is necessary, that the pressure of gas and radiation in the bottom layer be greater than the pressure of gas and radiation in the top layer by the quantity: dp = p_i+1 - p_i. The expression dp = dP / S is the equation of hydrostatic equilibrium. It can be rewritten in the form:

dp = dm * g / (4pr²) = -r * g * dr,
or shortly: dp/dr = -rg. (1)

where: r is a density on a distance r from the center of an object; g is an acceleration of free fall for given r; dm is a mass of a layer.

dm = - r * S * dr, (2)

(When we move from outside to the center, dr is negative, consequently, dm and dp are positive.)

Alas, the equation (1) is only fair for a homogeneous gravitational field, and for the object with non-colliding particles. It is not applicable to a spherically symmetric gravitating object. This mistake leads to a grandiose growth of pressure and density inside of planets and stars. So as the equation of hydrostatic equilibrium for spherically symmetric objects does not exist, or I did not met it earlier, it is necessary to deduce it here, proceeding from elementary principles. (That was my first proof of Ark Effect, logical proof. Several years later I have found another proves: analytical, mathematical, historical, computer modeling). So, on page the description with the help of figures 2-6 it was shown, that the formula (1) should not include the acceleration of a free fall g, but it must include the value v₀²/r - v_t²/r. Thermal velocity v_t coincides with the most probable velocity v_pr. If we use the average squared velocity v, than: v₀²/r - v_t²/r = v₀²/r - (2/3)v²/r. Let's name this value the absolute (or internal) acceleration of free fall, g_a.

g_a = v₀²/r - v_t²/r = g₀ - g_t, (3)

where: v₀ – orbital velocity of a particle for a given r; v_t – average thermal velocity of a particle; g₀ - Newtonian acceleration of free fall, or external acceleration of free fall, acceleration of free fall in vacuum. For Newtonian acceleration of free fall we can write:

g₀ = g₀M/r², (4)

where: g₀ - gravitational constant, renamed here as external gravitational constant, or gravitational constant in vacuum. The similar expression can be written down for absolute (internal) acceleration of free fall, acceleration of free fall in medium, without friction:

g_a = g_aM/r² = g₀ - g_t = g₀M/r² - g_t, (5)

Having divided (5) on M/r² we shell receive:

g_a = (g₀ - g_t )/(M/r²) = g₀ - g_tr²/M, (6)

Let's take the ratio of g_a to g₀:

g = g_a / g₀ = (g₀ - g_tr²/M) / g₀ = 1 - g_tr²/(Mg₀) = 1 - g_t/g₀ = 1 - (v_t/v₀)², (7)

Outside of the object, or far from the object, or in the vacuum cavity inside the object, the probe body will be drawn to the object with the force:

F = g₀Mm/r², (8)

The element of the object itself with the same regional density, which has the same temperature as the object, will be drawn to a part of the object, situated under a probe body, with the force:

F = g_aMm/r² = gg₀Mm/r², (9)

Let's compare expressions (8) and (9) to the Coulomb law for vacuum (10) and for medium (11):

F = (1/(4pe₀)) * Qq/r², (10)

F = (1/(4pee₀)) * Qq/r² = (1/(4pe_a)) * Qq/r². (11)

As we can see, the role of permeability of vacuum, or the role of the electrical constant e₀ plays the factor g₀; the role of relative permeability e plays the factor g, the role absolute permeability of medium e_a plays g_a.

To these strange analogies it is possible to add the following ones from electrodynamics:

em = (c/v)²; or if m = 1, then: e = (c/v)², (12)

And its analogue, the equation (7):

g = g_a / g₀ = 1 - (v_t/v₀)².

Consequently, g_a is a gravitational constant, applicable to a body, situated in a spherical layer of object, where the molecules of the layer have the average thermal velocity v_t, and with the same regional density. The average squared velocity can be defined from the equation: mv²/2 = 3/2*kT where: m - weight of a molecule of air; T - the temperature of gas (...). The value v_t can be find from equation v_t² = (2/3)v².

And g₀ is the gravitational constant in vacuum, which is applicable to a probe body far outside of attracting object.

At last, g is a relative gravitational permeability of a medium.

The equation g = g_a / g₀ = 1 - (v_t/v₀)² for the object with density, which is not equal to the regional density of the object, will have the coefficient r_object/r_probe. But main profit of this approach is in the demonstration of symmetries between the Newton and Coulomb laws. In fact such record of the formulae unites the attraction force in vacuum and repulsion force of Archimedes.

---

Stop correcting.

I don't correct the further 2000-text. I did not solve the riddle of my excellent formula G' = 1/exp(a + 1/a) yet.

Let's now return to a fine structure constant a, which is the running constant of the electromagnetic interactions, and to the early received gravitational constant, which in the normalized units is dimensionless, denoted there by G'; and it is the gravity fine structure constant:

G' = 1/exp(a + 1/a), (13)

The transition to SI units can be carried out under the formula:

G = (G'e³/(4sqr(a)e₀^3/2m_elm_pr²))^2/3. (13 a)

From this formula G is equal to 6.671479888E-11 N*m²/kg², that is in the perfect consent with the experimental value of G. According to CODATA-1999 the experimental value of G lays between 6.663E-11 and 6.683E-11 in SI units. According to CODATA before 1999 the experimental value of G was: (6.67259E-11 + /- 0.00085E-11) N*m²/kg². There is a question, why the accuracy of G has fallen? There is the second question, why for normalized units the formula 1/G ' = exp(a + 1/a) works, instead of, for example, the easier one: 1/G ' = exp(1/a)?

The answer consists in the following:
The quantity a can be regarded as the velocity of an electron in an atom of hydrogen, measured in the shares of the velocity of light.
The quantity (1 - a²) – is the relativistic amendment, which can be represented as (1-(v/c)²).
The ratio of quantities exp(1/a) and exp(a + 1/a) with good accuracy is equal to (1- a²) or to (1-(v/c)²).

Electron can be represented as a cloud, as an atmosphere of an atom, for which the gravigeometrical paradox works too.

That is why, the quantity G in old denotation, or g_? in new denotation is also the running constant. The expressions exp(1/a) and exp(a+1/a) just also must give 1/g_a' and 1/g₀'. But what correspondences between them are? Preliminary and, while what not the final analysis, gives:

It is obvious, that g₀ should be greater than g_a.

Hence, g₀' should be greater, than g_a'.

Hence, 1/g₀'should be less, than 1/g_a'.

(1/a) is less, than (a+1/a), and they both are more than 1.

Consequently: exp(1/a) is less, than exp(a+1/a).

At last we conclude, that:

1/g₀' = exp(1/a), or g₀' = 1/exp(1/a), (14)

1/g_a' = exp(a+1/a), or g_a' = 1/exp(a+1/a), (15)

Let’s try these results in SI units:

g₀= (g₀'e³/(4sqr(a)e₀^3/2m_elm_pr²))^2/3 = (e³/(4sqr(a)e₀^3/2m_elm_pr²))^2/3*(exp(1/a))^-2/3, (16)
g_a = (g_a'e³/(4sqr(a)e₀^3/2m_elm_pr²))^2/3 = (e³/(4sqr(a)e₀^3/2m_elm_pr²))^2/3*(exp(a+1/a))^-2/3, (17)
g = g₀/g_a = (exp(a+1/a))^-2/3/ (exp(1/a))^-2/3 = 1/exp(2a/3) = 0.995146913, (18)

g₀ = 6.704015058E-11 N*m²/kg²,
g_a = 6.671479888E-11 N*m²/kg².

In the expression (18) the relative gravitational permeability of a medium can be received through a constant a with good precision. On the other hand, we can check up this result applying the formula (7): g=1-(v_t/v₀)². In order to do this we must know the value of the orbital velocity: v₀=Sqr(g₀M/r) and the value of average thermal velocity of molecules of the air near the surface of the Earth v_t = Sqr(3kT/(29*a.u.m.)), where a.u.m.  – atomic unit of mass, 29 - molar weight of the air; and let T be equal to 300 K. Then:

v₀=7910 m/s; v_t = 508 m/s; G = 0.995876

This result does not absolutely coincide with the result of the formula (18) for several reasons:

1. The temperature 300 K is not very much approached to the real value of temperature. The check has shown, that for planets and stars we can receive rather good results.

2. The reason of discrepancy is contained also in that, that the sole value G, used in physics and astronomy now, actually in one cases "works" as g_a, and in the others - as g₀. So, between planets and stars the value g₀ works, but in the ground laboratories at pumped out air the value g₀ works, and at presence of the air the value g_a works. Last two items are correct, if we measure the force between the Earth and the probe body. But actually, the mass of the Earth is unknown, and we measure G between two probe bodies, between which the additive item g₀ works. All this confuses a situation at all.

Despite of these difficulties, it is necessary to move forward in the study of gravitation. This will unite the gravitation with electromagnetism. It, at the end, will simplify the understanding of gravitation. The experiment with the Gravity-Thermal Coil is extremely necessary. This experiment will show us the structure of the depths of planets and stars. This experiment will allow us to solve many energetic, ecological and technical problems.

The Arc Effect.

Russian Toroidal Matryoshka and press-nuclear reactions,