Как равномерно и однородно разбросать точки по сфере? Как задать скорости частиц и их проекции по осям в трехмерном пространстве?
Как равномерно и однородно на больших масштабах и хаотично на малых разбросать точки по сфере? Как задать скорости частиц и их проекции по осям в трехмерном пространстве? Я уже решал эту задачу 30 лет назад, а недавно просмотрел свои старые программы и подумал: а нет ли здесь ошибки? Почему здесь всё так просто? Почему так тупо:
z = 1 - 2·Rnd
Я не стал отягощать себя повторной попыткой проделать выкладки, а решил сверить свои результаты с тем, что уже есть в Интернете. Как оказалось, народ предлагает там массу бездоказательных советов, большинство из которых ошибочны. Поэтому я дам здесь краткое доказательство и код для генерации случайных координат на сфере, записанный на VB6, а вы мне кинете монетку на счет в Сбербанке. Это поможет мне поддержать свой сайт в живых и без рекламы. За всё это мне надо платить. В благодарность вам я кину сюда свои интересные находки по другим вопросам, таким как:
1. Как на компьютере решить систему уравнений, содержащих дифференциальные, интегральные, обычные и логических уравнения?
2. Как, имея несколько массивов данных, перенумеровать их по какому-то закону, чтобы программа была короткой и скоростной?
3. Как правильно заполнить ячейки частицами, если по условию задачи концентрация частиц на ячейку меньше единицы, но больше нуля?
4...Без монетки здесь не обойтись, так что вот номер моей карты на Сбере: 4276 3801 6293 1799. Спасибо!
Ну а теперь к выкладкам и доказательству.
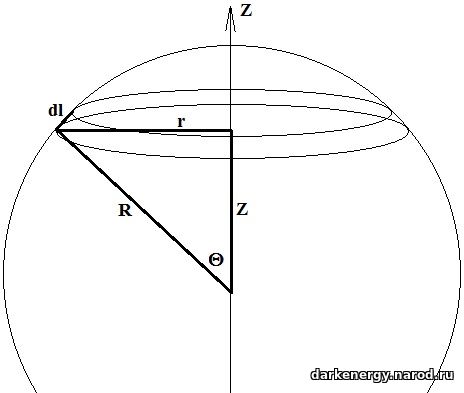
Возьмём арбуз и разрежем его не вдоль зелёных полосок, а поперёк, шаровыми слоями, дисками, скошенными на краях дисков. Шаровой слой арбуза — это часть арбуза, заключённая между двумя секущими плоскостями. Толщина скошенных дисков арбуза должна удовлетворять требованию: площади получившихся скошенных поверхностей всех слоёв арбуза должны быть одинаковыми.
Тогда, площадь корки арбуза в каждом слое будет определяться по формулам:
dS = 2πr·dl; r = R·Sinθ; dl = R·dθ. Объединив это, получим:
dS = 2πR2Sinθdθ.
Для того, чтобы убедиться, что dS мы записали верно, давайте проинтегрируем это выражение по зенитному углу θ от нуля до π радиан. Зенитный угол отсчитывается от оси OZ вниз. Можно также проинтегрировать по полярному углу от -π/2 до π/2. Полярный угол отсчитывается от плоскости XY вверх и вниз до оси OZ. Хотя однозначной терминологии здесь нет.
0∫π2πR2Sinθdθ = 2πR20∫π Sinθdθ = -2πR2Cosθ|0π = -2πR2·(-1-1) = 4πR2.
Сумма всех поверхностей корки арбуза дала площадь поверхности шара радиуса R.
Значение R для нас не имеет значения, и мы приравниваем его к единице. В итоге осталась площадь шара единичного радиуса, 4π.
Умножая её на случайную величину Rnd, принимающую любое значение от нуля до единицы, и приравнивая это к формуле, где ещё фигурирует угол θ, получим:
4π·Rnd = -2πCosθ|0θ.
Сокращаем на 2π:
2·Rnd = -Cosθ|0θ.
2·Rnd = -Cosθ + Cos0.
2·Rnd = -Cosθ + 1.
Cosθ = 1 - 2·Rnd.
θ = Arccos(1 - 2·Rnd).Мы получили случайный угол отклонения точки на сфере от положительного направления оси OZ. Тогда значением координаты z (или проекции vz) будет:
z = R·Cosθ.
Но R=1.
Получаем:z = Cosθ = Cos(Arccos(1 - 2·Rnd)).
z = 1 - 2·Rnd.
Ах вот оно в чём дело, и почему так тупо. Просто Cos и Arccos уничтожили друг друга.
Для скорости получим аналогично. Если скорость не равна единице, а некоторому значению V, то:
vz = V·Cosθ.
vz = V·(1 - 2·Rnd).
А если модули скоростей для всех частиц равны единице, то случайные проекции скоростей частиц на вертикальную ось будут определяться по этой простой формуле:
vz = 1 - 2·Rnd.
А теперь найдём случайные координаты x, y точек, разбросанные на сфере (или проекции скоростей для частиц vx, vy).
Для этого сначала найдём значение r = (x2 + y2)0.5 из условия x2 + y2 + z2 = 1.
r = (1 - z2)0.5.
Введем азимутальный угол φ. Он изменяется в пределах от 0 до 2π. Диапазон от нуля до 2π умножим на Rnd. Результат обозначим, к примеру, буквой q = 2πRnd и получим:
x = r·Cos(q); y = r·Sin(q).
Для проекций vx, vy скоростей V получим аналогично.
Сначала запишем маленькую v = (vx2 + vy2)0.5, являющуюся проекцией вектора V на плоскость XOY.v = (V2 - vz2)0.5.
vx = v·Cos(q); vy = v·Sin(q).Замечание: Не все браузеры правильно отображают греческие символы, особенно это касается смартфонов. Так что извините, если где-то что-то отобразилось не так, как я хотел. Извините также за очепятки, если таковые имеются.
Случайное разбрасывание галактик на сфере, которое я делал для объяснения геометрии замкнутой вселенной смотрите на странице Замкнутая Вселенная.
Здесь показан мой метод воображения Замкнутой Вселенной. Сейчас мне известны еще два метода. Все эти методы дают одни и те же числовые результаты, а значит, все верны и дополняют друг друга.
Галактики во Вселенной разбросаны хаотично, но однородно на больших масштабах. Если Вселенная замкнута, то мы сначала разбрасываем точки на сфере. Заставляем компьютер нарисовать спиральки-галактики в этих точках. Затем мысленно прокалываем сферу в нижней точке и растягиваем этот прокол во все стороны так, чтобы все радиальные длины масштабы сохранялись. Таким образом, мы получаем сечение Замкнутой Вселенной в плоскости xy. Галактики, которые мы рисовали на сфере, проектируются на эту плоскость. Аналогично получаем сечения yz и zx.
Вопросы:
1. Что бы Вы увидели в Замкнутой Вселенной, если бы Вы могли видеть неограниченно далеко?
Подсказка: Учёные люди говорят — собственный затылок.
Но так ли это? Кидайте монетку, и я отвечу Вам на этот вопрос 4276 3801 6293 1799.
2. Если электрон быстренько облетит всю Вселенную по прямой, то кем он вернётся? Электроном или позитроном? Как по поводу фотонов? Протонов? За Ваш убедительный ответ я сам Вам монетку вышлю. Давайте номер Вашей карты Сбербанка.
Случайное распределение скоростей по направлениям я многократно использовал для доказательства Эффекта Арки в программе Аркбол на странице Полые планеты и звёзды. Эффект Арки и космология. Программа Аркбол.
Спасибо за прочтение и хорошего вам настроения!