ЧЕТЫРЕХМЕРНОЕ ВРАЩЕНИЕ

(Часто Задаваемые Вопросы п.10.
Космическая Генетика)

13, 14 марта 1999 г.

IK.: А что вообще такое сабж? Че-то никак себе пpедставить не могy...
MF.:Я так понимаю, что к стандаpтной тpезмеpной системе коpдинат добавляется четвеpтая ось - вpемя...
Anton E.: Гocпoди, зaчeм ты этo cпpocил. Ceйчac нa yчacтникoв вывaлитcя тaкoй пoтoк бpeдa. He тpoжь Ивaнa Гopeликa - бpeдить нe бyдeт. ИMXO зoлoтaя иcтинa...
IK.: А даже если и бpед, все pавно интеpесно. Мне нpавятся абстpактные наyки и теоpии. Тем более, что пока я не выслyшал теоpию, я не могy сyдить о ее pеальности. Кстати, в споpе pождается истина...
ML.: О СТО pечь? Пpостpанственно-вpеменной повоpот подpазумевает изменение скоpости...
PS.: Hе обязательно. Почему именно время? Система координат - это просто набор чисел. Как тебе такая трехмерная система координат: первая координата - возраст человека, вторая - его рост, третья - его вес? Каждый человек будет представляться точкой в этой системе координат. И в ней, естественно, возможно вращение... Можно добавить четвертую, пятую и т.д. координаты - например, ширина бедер, дата рождения в днях от Рождества Христова,..
AA.: Hy а если все же не pассматpивать весьма абстpактное возpастно-pосто-весовое пpостpанство и емy подобные, а веpнyться к обычномy? И если пpи этом не касаться также и вpемени. Что совpеменная астpофизика говоpит о четвеpтом _пpостpанственном_ измеpении? Или подобных вопpосов она не касается (я сам не астpофизик)?...
PS.: Я тоже не астрофизик. Hасколько я знаю, современная астрофизика говорит, что у нашего пространства три измерения. Есть, правда, экзотические теории, где число измерений доходит до 20 с лишним, причем все они, кроме трех, свернуты в трубки очень малого диаметра. Это как цилиндрическая поверхность в случае двух измерений. У нее два измерения - вдоль оси цилиндра и угол поворота вокруг этой оси. Hо если диаметр цилиндра очень маленький, мы можем ничего не знать о втором измерении и считать его одномерным - прямой линией.

Вопрос Игоря действительно очень сложный. Требует развёрнутого ответа.
Во избежание "съёзда крыши" Антону рекомендую воздержаться от чтива.
План
1.Многомерные и замкнутые пространства.
2.Является ли пространство Вселенной трёхмерным?
3.4-мерное вращение в Космической Генетике.

1.Многомерные и замкнутые пространства.

Вообразить 4-мерное пространство привычным способом не удастся. Однако существует очень простая процедура позволяющая не только воображать, но и рисовать четырёхмерные фигуры. Для этого сначала берём трёхмерное пространство, xyz, в нём лист бумаги - двумерное пространство xy. Hа листе рисуем, к примеру квадрат, стороны которого, попарно параллельны осям x и y. Берём другой лист и "вгоняем" в него третье измерение s. С осью s отождествляем цвет, то есть, ставим в соответствие видимому спектру тот диапазон расстояний, который будет удобен при рисовании. Цветовую ось можно считать бесконечной, сопоставляя, к примеру направление в ультрафиолет положительным, а направление в инфракрасную область, отрицательным. Берём цветные карандаши и рисуем квадрат, стороны которого попарно параллельны осям x и s. Очевидно, два отрезка разного цвета накладываются друг на друга. Для удобства просмотра рисунка мы рисуем их рядом, но имеем в виду, что на нашем листе они совпадают. Концы этих отрезков, скажем синего и красного, соединяем друг с другом короткими отрезками, цвет которых монотонно переходит от синего к красному. (синий-голубой-зелёный-желтый-оранжевый-красный). Сравним два листа, на одном имеем квадрат, нарисованный простым карандашом, на другом тот же квадрат, но он почему-то напоминает нам обычный отрезок. Поворачиваем первый лист, так чтобы видеть его в ребро и убеждаемся что рисунки теперь почти совпадают. Рисуем другие плоские фигуры на обеих листах. Убеждаемся, что вся обычная геометрия правильно работает в обоих случаях.

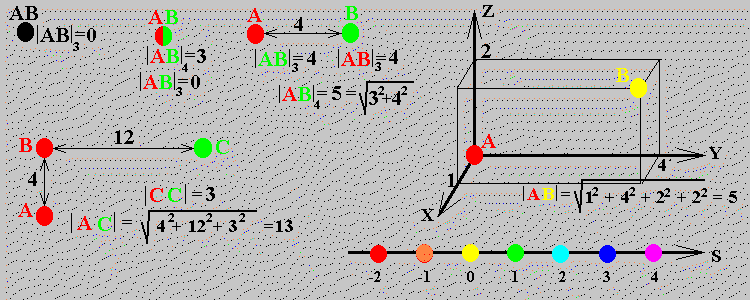
Вспоминаем, что на двумерном листе мы можем рисовать простым карандашом трехмерные фигуры, к примеру, куб. Без проблем, с помощью цветных карандашей рисуем 4-мерный куб. После определенных тренировок можно научиться правильно рисовать 4-мерные фигуры, ребра которых уже не являются параллельными осям. Становятся понятными очень любопытные парадоксы четырёхмерной геометрии. К примеру, как нужно повернуть правый трёхмерный ботинок, чтобы получить из него левый трёхмерный ботинок. Можно нарисовать игру

Перейти на рисование 5- и выше мерных пространств можно сопоставляя при рисовании толщину, волнистость, прерывистость линии.

Мне раньше казалось, что это я сам изобрёл метод представления четвертой пространственной координаты цветом, однако потом я где-то прочитал, что какой-то французский математик работает этим же методом.

Перейдем к замкнутым пространствам. Если не касаться чисто математических хитростей, а рассматривать реальное пространство Вселенной, то я сейчас могу привести три вида замкнутых пространств. (Может быть их и больше, но пока сам не "переизобретёшь", не поверишь.)
а. сферическое,
б. эллиптическое,
в. замощения.
Наиболее правдоподобным сейчас представляется "эллиптическое" замкнутое пространство. Однако другие виды исключить пока нельзя и, кроме того, наиболее простым переходным оказывается сферическое замкнутое пространство. К "эллиптическому" пространству переход предельно прост и его название не совсем соответствует истине. Со словом "эллиптическое" сразу ассоциируется некий эллипсоид вместо сферы. Однако, на самом деле, чтобы перейти от сферического замкнутого пространства к эллиптическому замкнутому пространству необходимо лишь отождествить диаметрально-противоположные точки на сфере. Если бы планета Земля имела "эллиптическую" геометрию, то мы убираем, к примеру с Западного полушария все материки и океаны, а помещаем туда копии материков и океанов Восточного полушария. Все плавно стыкуем и получаем две Африки, две Европы, две Азии, две Москвы, два Антона Е., если он живет в России, ни одного ПТ, если он живет в Бразилии, два Солнца, если сейчас в России день. Но, поскольку два Антона на самом деле одно и то же лицо, и видят они "не два Солнца", а одно и то же, то заключаем, что в "эллиптической" геометрии полный телесный угол равен не 4*pi радиан, а 2*pi радиан. Площадь поверхности Земли будет не 4*pi*r^2, а 2*pi*r^2, Объём Земли будет не 4/3*pi*r^3, а 2/3*pi*r^3. Это было введением по поводу отличия эллиптического мира от сферического мира.

Теперь попытаемся вообразить замкнутый сферический мир. Можно конечно использовать медод А.Эйнштейна. том2. стр. 90-93. Однако это трудный метод. У него большая голова и он сумел уместить в неё получаемый бесконечный рисунок из конечной сферы. Моя голова поменьше и мне пришлось изобрести свой метод. Не переживайте результаты те же. Итак мы с Альбертом берём по сфере. Альберт берёт стеклянную, я беру резиновую, рисуем на ней: Альберт кружочки, я галактики. Ставим свои сферы на плоские столы, я на конечный, Альберт на бесконечный. Ставим по наблюдателю на сферы, Альберт внутри сферы в самую низкую точку, я на верх сферы. Альберт цепляет лампочку в верхнюю точку сферы и смотрит на тени получаемые от кружочков на бесконечном столе. Я прокалываю иглой свою сферу и растягиваю сферу за отверстие так, чтобы сохранить длину меридианов неизменной, и чтобы сферу распластать и положить на стол. Итак мы имеем плоские разрезы одной и той же Вселенной, у сферы Альберта деформировались радиальные и тангенциальные размеры, у моей сферы деформировались только тангенциальные размеры. Дополняем полученные разрезы Вселенной двумя взаимно-перпендикулярными разрезами, выбрасываем по одной восьмой в мусорное ведро, и получаем замкнутую Вселенную с вырезом. В центрах по наблюдателю. От наблюдателей идут оси x, y, z. Вселенная однородна, значит центр условное понятие. Мы могли поставить наблюдателя в любую точку исходной сферы. Проводим вычисления, Альберт по своим формулам, я по своим. Поскольку исходные сферы у нас были те же, поскольку деформации на самом деле не поддаются замерам наших наблюдателей (вокруг них в непосредственной близости пространство не деформируется, а остается практически тем же), то не удивительно что результаты у нас оказываются теми же.

Так объем замкнутой "сферической" Вселенной оказывается равным 2p²ρ³, ρ - радиус кривизны. Объем замкнутой "эллиптической" Вселенной будет в два раза меньше. "Сферическую" Вселенную, где я выбросил не одну восьмую, а половину см. на страничке:
Итак вопреки тому, что многие говорят и пишут, что замкнутое пространство вообразить нельзя, мы убеждаемся в обратном. Оказывается, можно и не только вообразить, но и рисовать, и даже разными способами. Два уже были показаны, как "метод Альберта" и "мой метод 1". Теперь, вспоминая о методе рисования четырёхмерного пространства с помощью цвета, получим "мой метод 2" для рисования
замкнутого пространства. Рисуем сферу на листе цветовым методом. Сфера есть объект, точки которого мы можем задать в трёхмерном пространстве с помощью координат x, y, z по формуле x²+y²+z²=ρ². Заменяем вертикальную координату z на цветовую s. Обана!, наша резиновая сфера, с нарисованными на ней галактиками сразу же падает на поверхность стола без всякого прокалывания и растягивания. Мы замечаем, что рисунок должен быть следующим: в центре синий наблюдатель, около него голубые галактики, дальше зеленые, желто-зелёные потом снова ближе к наблюдателю желтые, оранжевые и наконец, диаметрально-противоположные галактики мы рисуем около, или прямо на наблюдателе красные галактики. (Переделаю это предложение в случае эллиптической геометрии: в центре синий наблюдатель, около него голубые галактики, дальше зелёные, желто-зеленые, потом снова, ближе к наблюдателю желтые накладываются в точности на зеленые, оранжевые накладываются в точности на голубые, красный наблюдатель накладывается в точности на одного и того же синего наблюдателя.) Сравни два абзаца ниже:

Разрез замкнутой СФЕРИЧЕСКОЙ Вселенной представляет собой круг каждая точка которой является двумя точками, отстоящими друг от друга очень далеко R=pρ, которые просто проектируются друг на друга. Эти точки лежат на цветовой координате, но она ничем не хуже пространственной, поскольку мы можем заменить любую координату x, y, z на s, то есть, делаем вывод, - направление на самую удаленную точку В от некоторой исходной точки А имеет нулевую проекцию на все оси x, y, z и полностью совпадает с невидимой нами осью s. То есть, самый далекий объект просто проектируется на наблюдателя но никак с ним не связан.

Разрез замкнутой ЭЛЛИПТИЧЕСКОЙ Вселенной представляет собой круг, каждая точка которой является двумя точками, отстоящими друг от друга очень далеко, R=pρ, которые просто проектируются друг на друга. Эти точки лежат на цветовой координате, но она ничем не хуже пространственной, поскольку мы можем заменить любую координату x, y, z на s, то есть, делаем вывод, - направление на самую удаленную точку В от некоторой исходной точки А имеет нулевую проекцию на все оси x, y, z и полностью совпадает с невидимой нами осью s. То есть, наблюдатель может быть представлен как совокупность частиц, у которых три пространственные координаты совпадают, но по четвёртой координате каждая частица представлена как под и антипод. Если это одно и то же, то дальше никаких спекуляций. Если это не одно и то же, то здесь широкое поле для гипотез, и их проверок. Может быть под и антипод это ячейки для частицы и античастицы, может быть это протон и электрон, может быть это ячейки для электрона и позитрона, может быть это уровни для частиц со спином 1/2 и -1/2, или 1 и -1, и т.д. Во всяком случае, появление данного гена в структуре пространства полезно для объяснений, но пока нет четкой ясности что же это такое, то в КГ нет и конкретных утверждений. (Добавлено в марте 2000: Скорее всего реален мир с отождествлением точки и соответствующего ей экватора.)

Итак, мы имеем круг, в каждой точке которого имеется две точки.
x²+y²+s²=ρ²

Он весь ограничен желто-зеленой окружностью
x²+y²=ρ², s=0.
Этот круг нарисован на листе, где мы приняли z=0.
Очевидно, что полный рисунок можно будет получить разбивая уравнение x²+y²+z²+s²=ρ², по кускам в зависимости от значения z. Поднимаясь и опускаясь с листа, то есть, увеличивая и уменьшая z, мы получаем новое представление замкнутого мира "мой метод 2". Это опять же можно не только вообразить, но и нарисовать.

(К сожалению я пока не нарисовал его в электронном виде и пока не поместил на сайт.)
Рисунок удобно получить, повернув первый круг под некоторым углом, а затем нарисовать по три четверти новых кругов изменяя значение z, с учетом того, что z есть уже та третья координата которую мы с успехом рисуем на двумерном рисунке.

Анализируя результаты интегрирований, для вычисления объемов и площадей, анализируя рисунки, приходим к выводу, что наша замкнумая трёхмерная Вселенная является обычной трёхмерной гиперсферой в открытом (или замкнутом*) 4-мерном пространстве.
* окружность, то есть замкнутое одномерное пространство можно нарисовать не только на открытом двумерном простраснстве, то есть, на плоскости, но и на замкнутом двумерном простраснтве, то есть, на сфере.

Сравнивая методы воображения рисования одной и той же замкнутой Вселенной, приходим к выводу, что все они полезны, как в черчении вид спереди, вид сбоку, вид сверху и т.д. Везде можно указать ход лучей, указать координаты, менять привычные пространственные координаты на цветовую. Приводя координатные оси в движение, мы получаем, некоторое подобие четырёхмерного вращения.

2.Является ли пространство Вселенной трёхмерным?

Хотите точно? Пожалуйста:
Размерность пространства не 3, не 4, ни 10, ни 25, а N=3.0909*10^20.
В этой шутке есть доля правды.
Однако, всё по порядку.
Рассмотрим два континуума.

Континуум 1.
Обычное пространство, в котором мы наблюдаем изменения с течением времени. Все предметы, окружающие нас, движутся во времени. Стена комнаты оказывает на нас влияние в момент времени, когда свет доходит от стены к тому месту, где находимся мы. Но та же стена, которая была мгновение раньше, или, которая будет мгновением позже, влияния не оказывает. Её просто нет в данном временном сечении пространственно-временного континуума. Разбивая время на дискретную последовательность, скажем на микросекунды, и ставя в соответствие каждой микросекунде определенную ориентацию предметов, плавно соединяя сечение к сечению, мы получаем пространственно-временной континуум 1. Если считать скорость света бесконечной, то континуум будет одинаков для всех наблюдателей. Если скорость света конечна, то для каждого наблюдателя, покоящегося друг относительно друга, но расположенных в разных точках пространства, пространственно-временные континуумы будут иметь тем большую разницу, чем дальше друг от друга находятся наблюдатели. (Дописано март 2000: здесь лучше говорить не континуум, а дискретное пространство-время.)

Континуум 2. Из СТО мы видим, что пространство и время перестали существовать как независимые сущности. Они слились в единый континуум, описываемый геометрией Минковского. Сечениями этого 4-мерного континуума являются 3-мерные пространства в каждом из которых время течет своим темпом. Эти сечения образуют друг с другом углы, величины которых определяются относительной скоростью данных сечений. Изменяя скорость, мы совершаем поворот в пространстве-времени Минковского. Разбивая скорость на дискретную последовательность, скажем по одному метру в секунду*, ставя в соответствие каждой скорости определённую пространственно-временную ориентацию предметов, плавно соединяя сечение к сечению, мы получаем пространственно-временной континуум 2. Он будет для каждой исходной точки трёхмерного пространства индивидуален.
(* разбивка скорости по одному метру в секунду не значит, что мы получим ряд из 2*с сечений. Это становится понятно, если вспомнить закон сложения скоростей в СТО)

Итак, казалось бы, поскольку мы получаем более чем трёхмерные пространства, почему мы наблюдаем трехмерное пространство?
А что представляет собой наблюдатель?
Совокупность частиц, беспорядочно движущихся с разными скоростями.
Следовательно, с каждой частицей может быть поставлена в соответствие своя система отсчета, в которой частица покоится. Тогда каждая частица "видит" окружающий мир по-своему, чисто индивидуально. Отличия в картинках "наблюдаемых" частицами будет тем больше, чем больше относительные скорости частиц, то есть, чем выше температура объекта. А если температура ниже, то картинки оказываются всё более и более подобными. Наконец наступает сверхпроводимость, когда картинки "видимые" всеми электронами образуют узкую полосу, которая не пересекается с полосой картинок "видимых" атомами решётки. Другими словами электроны проводимости живут в пространстве А, а атомы решётки в пространстве В. Аналогичный процесс, связанный с преобразованиями размерности может проявляться в явлении сверхтекучести. Еще одно явление предсказано в КГ - сверхплотность, а точнее, скачкообразное уменьшение объёма охлаждаемого вещества. Образно говоря, в стакане, наполовину заполненном водой и наполовину - подсолнечным маслом при некоторой температуре происходит проваливание масла в воду, а еще ниже протекание стакана. При сверхнизких температурах стекло занимает пространство А, вода занимает пространство В, масло занимает пространство С. А при обычных температурах все эти вещества занимают пространства А, В, С и мешают друг другу. Это был упрощенный пример, однако я не удивился когда узнал, что в прошлом году (1997г) физики были удостоены Нобелевской премии за открытие дробного заряда. Главный принцип - сверхнизкие температуры и подавление привычных измерений.

Из всего выше сказанного следует, что размерность пространства наблюдаемая макроскопическим объектом, то есть, нами, не обязательно остается той же при движении на масштабы вглубь материи.

К аналогичным выводам можно прийти из разных разделов физики. Так же как СТО, квантовая механика оперирует и немыслима без комплексных величин. Это явно указывает на наличие дополнительного пространственного измерения в микромире, которое становится незаметным, а следовательно мнимым для макроскопического наблюдателя. Квантовая механика даёт в решениях спектры энергетических уровней. Эти спектры напоминают спектры систем отсчета в СТО.

В последней опубликованной работе А.Эйнштейна читаем последний абзац. Том 2, стр.873
"Можно убедительно доказать, что реальность вообще не может быть представлена непрерывным полем. Из квантовых явлений, по-видимому, следует, что конечная система с конечной энергией может полностью описываться конечным набором чисел (квантовых чисел). Это, кажется, нельзя совместить с теорией континуума и требует для описания реальности чисто алгебраической теории. Однако сейчас никто не знает, как найти основу для такой теории."

Я бы заменил предпоследнее предложение следующим образом:
Теория континуума построенная А.Эйнштейном работает на макроуровне, однако при переходе на микроуровень континуум 3+1 необходимо заменять решеткой, которая только приближённо выглядит как 4-мерная. На самом деле самый малый элемент решётки есть квазизамкнутая окружность, или виток спирали. Квазизамкнутая окружность образована пересечением N линий и имеет соответственно N рёбер. Данное N дает дискретный спектр скоростей и, в то же время, дискретный поворот. Перенося ребра параллельно в единую точку мы получим репер возможных направлений и скоростей для определенной частицы, являющейся на самом деле дефектом решётки, недостающим или лишним звеном решетки.

После создания ОТО А.Эйнштейн всю оставшуюся жизнь пытался объединить гравитацию и электромагнетизм. Неоднократно возвращался к идеям пятимерного континуума, предложенного Калуцей и Клейном. Перефразировал пятое измерение из цилиндричного в замкнутое, периодическое и вновь отбрасывал его, хотя уже и оставлял в своем 4-мерном континууме 5-мерные вектора. Эти подходы давали возможность записывать в одних уравнениях величины описывающие гравитацию и электромагнетизм, однако не давали ни зарядов, ни других констант, ответственных за электромагнитное поле.

Кажется этого и не должно было случиться, ибо Великий геометризатор так и оставил частицы шариками, или материальными точками. Только представление пространства-времени Вселенной как сложный, но в высшей степени симметричный клубок линий может привести к желанному результату.

Эйнштейн проявлял недовольство в связи с тем что 5-мерный континуум был не симметричен по пространственным координатам. Одно измерение оказывалось очень маленьким и замкнутым, по сравнению с другими, которые он называл открытыми, хотя на самом деле, они тоже были замкнуты.

В КГ выявлена одна удивительная вещь возвращающая симметрию. Мы живем в трёхмерном пространстве и ощущаем поток времени. Что такое время. Это и есть последовательная совокупность оборотов по одному из измерений, когда уже обратного хода нет. Пространство микромира можно представить имеющим 4 пространственные координаты имеющие разный радиус кривизны. Один оборот по наименьшему измерению соответствует одному временному сечению. Время абстрактно, нереально, представлено совокупностью оборотов.

Это же вращение делает пространство изотропным. Взгляните на лист в клетку явная анизотропия. Такую же анизотропную картину получим в трехмерной и четырехмерной решетках. Однако вращение по четвертой координате, даёт время, и даёт изотропию рёшетки.

Но покоя нет, а значит существует вращение и по другим замкнутым координатам.

Итак, с одной стороны, мы получаем, что при переходе в микромир пространство может оказаться более чем трехмерным. С другой стороны, вспоминая аналог перехода от сферического мира к "эллиптическому", когда два Антона Е., наблюдали из двух Европ два Солнца, один в Восточном полушарии, а другой в Западном полушарии, и учтя что Антон Е. это одно лицо, и, который, проводя измерения в непосредственной близости, определяет объем шара, как 4/3*pi*r^3, а мы получили для больших масштабов на "эллиптической" Земле 2/3*pi*r^3, то заключаем, что при переходе на большие масштабы мы можем иметь замощения, которое подобно уменьшению размерности, но не является таковым.

Пару слов о гипотезе замощений во Вселенной.
Замощения возможны в пространстве с нулевой и ненулевой кривизной.
В случае замкнутого мира вариант "эллиптической" геометрии даёт две идентичные полусферы. То есть, полный объем ровно в два раза меньше, чем объем сферического мира. Если предварительно разбить сферу на n одинаковых фигур, как футбольный мяч, то в мире будет в точности n Антонов Е., и если он имеет хороший телескоп, то он увидит себя же, в разных участках неба несколько раз, правда помоложе, а точнее далеких-далеких своих предков.

Если пространство плоское, кривизна равна нулю, то можно получить ячеистую Вселенную, каждая ячейка которой является копией соседней. Вообразите, что Вы сидите в комнате со стеклянными стенами, во все стороны от вашей комнаты, такие же комнаты, там стоят такие же столы как в вашей комнате, за каждым столом сидите опять же Вы. Если Вы попытаетесь перехитрить и пойдете, скажем в левую комнату, то тот Вы, который был в левой комнате пойдет в следующую левую комнату, а тот который был в правой комнате, пойдет в Вашу исходную комнату. Если Вы решите застрелиться, то это произойдет во всех комнатах, то есть, нет смысла рассматривать все комнаты. Кстати, Антон может застрелиться даже не целясь себе в висок, а выстрелить в того Антона, что на три этажа выше, двумя комнатами левее, и одной вперёд...

Объем такой Вселенной оказывается a*b*c. Такая Вселенная интересна тем, что она: замкнута, откуда вышел туда и пришёл, конечна, V=a*b*c, безгранична, стеклянные стенки условны, евклидова, параллельные прямые, всегда параллельны.
(Кто автор гипотезы замощений во Вселенной? Случайно не я?)
Наблюдательные данные в астрономии пока ничего не говорят о наличии порядка замощений или духов, тыльных сторон галактик. Тем не менее, лично мне, представляется наиболее вероятной "эллиптическая" геометрия Вселенной, но я не удивлюсь, если окажется, что мы давно наблюдаем Млечный Путь в нескольких точках неба одновременно, но их вид отличается друг от друга из-за того, что Солнце расположено не в центре Млечного Пути, а также из-за того, что пока свет доходит от одной копии до другой с ней происходит значительная эволюция до неузнаваемости.

Отвечая на поставленный выше вопрос, "Является ли пространство Вселенной трёхмерным?" скажем: Вероятно да, но это справедливо на масштабах, сравнимых нашим. Переходя на другие масштабы, представление о размерности смазывается, увеличивая измеряемую сферу, мы можем наткнуться на точки, которые уже были включены внутрь малой сферы, а уменьшая размеры сферы, мы можем наткнуться на раздваиваемые или размножаемые точки, и мы говорим о пространстве A, B, C.., что подобно появлению новой размерности.

Во избежание возможных недоразумений в терминологии я отделяю четырёхмерное вращение в КГ от других возможных спекуляций по поводу многомерного вращения.

Весь клубок линий Вселенной, или полная структура пространства-времени в КГ пока не известна. Она выстраивается по отдельным генам - геометрическим образам, таким как:
* квазизамкнутая окружность,
* замкнутый сферический мир,
* замкнутый эллиптический мир,
* цветовое представление,
* метод замощений,
* совокупность ИСО, как система энергетических уровней,
* представление гравитационного взаимодействия как переход с уровня на уровень (из ИСО1 на ИСО2) при недостатке звена в пучке линий, пронизывающих квазиокружность (частицу),
* представление электромагнитного взаимодействия как синхронный поворот линий, пересекающих квазиокружность, а также, как превращение ячейки типа А в тип В,
* представление времени как дискретная совокупность оборотов, при котором, если некоторое движение происходит несколько раз за один оборот, то данное движение обратимо, если же некоторое движение происходит в течении дольше, чем один оборот, то движение необратимо, что превращает пространственную координату во временную для макрообъектов или макрособытий, а также, через выбор наиболее выгодного энергетического решения, объясняет направленную работу мозга, синергетику, и так далее,
* представление частиц, как недостатки или избытки звеньев решётки, или их совокупностей, движущихся по квазиокружностям,
* представление массы или инертности, как функцию угла, который составляет квазиокружность (виток спирали) определенного типа частицы к пространству макроскопического наблюдателя, то есть, массы нет, все звенья одинаковы, разница в массе проявляется из-за разного угла квазивитка по отношению к нам, а соответственно, чем меньше угол, тем меньше проекция квазивитка на пространство наблюдателя, тем больше витков должна пройти частица для получения некоторого определенного, измеряемого нами, ускорения,
*** и т.д.

К четырехмерному вращению КГ придем также по наиболее простым генам.

Рассмотрим обычное вращение в 4-мерном евклидовом пространстве

(x, y, z, s, t). Для того, чтобы вообразить его, нарисовать, или смоделировать на компьютере, одну из пространственных координат s отождествим с цветом. Пусть мы имеем две частицы, одна из которых, скажем ядро, находится в начале координат (0, 0, 0, 0), другая, электрон, вращается вокруг ядра.

Вариант вращения в плоскости xy.
Очевидно, данное вращение в 4-мерном пространстве вточности проектируется на видимое нами пространство (x, y, z, t).
Запишем его четыре фазы для второй точки:
4-мерное + время
(1, 0, 0, 0, 0)
(0, 1, 0, 0, 1)
(-1, 0, 0, 0, 2)
(0, -1, 0, 0, 3)
3-мерное + время
(1, 0, 0, 0)
(0, 1, 0, 1)
(-1, 0, 0, 2)
(0, -1, 0, 3)
Вариант вращения в плоскости xs.
Данное вращение в 4-мерном пространстве проектируется на видимое нами пространство (x, y, z, t) как колебание:
4-мерное + время
(1, 0, 0, 0, 0)
(0, 0, 0, 1, 1)
(-1, 0, 0, 0, 2)
(0, 0, 0, -1, 3)
3-мерное + время
(1, 0, 0, 0)
(0, 0, 0, 1)
(-1, 0, 0, 2)
(0, 0, 0, 3)
В моменты времени t=1, t=3 координаты трёхмерного пространства совпадают, то есть, ядро и электрон находятся в одной и той же точке. Возможно ли это. Да, если четвертая пространственная координата действительно существует. Именно по ней в данный момент координата s для электрона и ядра различны.

Как это нарисовать? Нулю по координате s ставим в соответствие, к примеру, зеленый цвет, единице - голубой, минус единице - желтый цвет. Тогда серия из 4-х картинок выглядит так:
-----ядро---------------------- электрон----
(0, 0, 0, зеленый, 0) ---- (1, 0, 0, зелёный, 0)
(0, 0, 0, зеленый, 1) ---- (0, 0, 0, голубой, 1)
(0, 0, 0, зелёный, 2) ---- (-1, 0, 0, зелёный, 2)
(0, 0, 0, зелёный, 3) ---- (0, 0, 0, желтый, 3)

Любопытную картину вращения можно получить моделируя вращение кристаллической решётки в плоскости xy, относительно гипероси zs, а также в плоскости zs, относительно гипероси xy. Картинка уже получится наглядной если по четырем координатам взято по две частицы. Всего в этом случае 8 частиц.

Интересны варианты при замыкании четвертой координаты:
...к, о, ж, з, г, с, ф, к, о, ж, з, г, с, ф, к...
а также при колебаниях по ограниченному четвертому измерению:
...к, о, ж, з, г, с, ф, с, г, з, ж, о, к, о, ж...

Сочетание циркуляции по замкнутой четвертой координате, или колебаний по ограниченной четвертой координате представляются интересными и в сочетании с движениями по другим осям напоминают
сложные вращения.

В данном подходе далее появляется большая свобода для гипотез, и поэтому, пока ограничимся вышесказанным.

Единственное что мы отсюда выносим - зто постулат о том, что при совершении одного акта циркуляции ...к, о, ж, з, г, с, ф, к, о... , либо одного акта колебания ...к, о, ж, з, г, с, ф, с, г, з, ж, о, к, о,.. по четвертой пространственной координате выражается в природную единицу времени t0. Для макроскопического объекта наших масштабов t0=0.00136 секунды. (Вывод ниже.) То есть, мы имеем 4-мерное пространство, проектирующееся для макрообекта в 3-мерное пространство и время.

Когда возникло подозрение о том, что временная координата на микроуровне вырождается в пространственную, по которой частицы могли двигаться вперёд и назад, тогда возник и вопрос а как выразить единицы измерения? Мы пользуемся в системе СИ в качестве единиц длины метрами, а в качестве единиц времени секундами. Будет ли четырехмерная фигура 1м*1м*1м*1с четырехмерным кубом. Вероятно нет. Если мы уберём метры или секунды, то мы уйдем из системы СИ. А если попробовать совершить поворот, значит связь с СИ останется, а многие формулы должны упроститься. Значит нужна некоторая универсальная единица длины-времени. Обозначим её [!]. Она должна работать при таком повороте нашего трехмерного пространства и времени, когда длина пространственой и временной координат замкнутой Вселенной будут численно равны. То есть, в таких единицах, когда Х'=Y'=Z'=Т'. В то же время квазиокружность по любой из координат должна содержать одинаковое число ребер N, то есть: N=X'=Y'=Z'=T'. Звено квазиокружности движется со скоростью с, но проекции всех этих звеньев на одну из линий этой квазиокружности дают спектр из 2*N инерциальных систем отсчета, движущихся друг относительно друга с самыми разными скоростями от -с до с. Оказалось, что в этих нормированных единицах выполняется равенство N=X'=Y'=Z'=T'=1/H'=1/h'=1/f'=1/l'=3.0909*10^20, где
Н' - постоянная Хаббла,
h' - постоянная Планка,
f' - квант силы,
l' - комптоновская длина волны протонной квазиокружности,
Переходный коэффициент t0 и его производные граничная частота 1/t0, и граничная длина c*t0 вошли во многие формулы. Предварительный перечень формул приведен на странице, где из трёх известных констант, теоретически выведены остальные. Спектр ИСО, квазизамкнутая окружность, интерпретация постоянной Хаббла, как угловой скорость света в об/сек. даны на странице

Итак, четырехмерное вращение в КГ представляет собой циркуляцию квазизамкнутых координатных осей. Вращение наименьшей координатной оси вырождается во время для макроскопического наблюдателя. Дефекты и их совокупности, вращающиеся по разным квазизамкнутым окружностям, представляют собой
частицы разного типа.

Свет, идущий от далеких галактик, приходит к нам повернутым тем сильнее, чем дальше галактика. С другой стороны, КГ предсказывает, что большую часть (Р)еликтового (И)злучения составляет Солнце. То есть, часть РИ есть Солнце наизнанку в пространстве-времени, в котором есть вклад и за год назад, и за миллион лет назад, и за миллиард лет назад... То есть, РИ также есть результат вращения решётки.

КГ находится в состоянии постоянного развития. Многие её выводы будут уточнены, некоторые могут оказаться ошибочными. Однако главный её стержень - четырехмерная замкнутая решётка, есть то направление, которое приведет к успеху.

Эта страница была написана в 1999 году.

Продолжение "Часто Задаваемые Вопросы"

К оглавлению Космической Генетики

Иван Горелик