Solar Energy Sources. Part 1.
Part 2 has not yet been translated. See its Russian version. There you will see that the luminosity of stars is described by Hawking's formulas for the "temperature of black holes", or by Unruh's formula for an accelerated rod.
The probable source of stellar energy is proposed here. This result was received in 1998, but it does not accepted yet by the scientific community. The probable cause is hidden in the difficulty of Bell's paradox. In order to understand the energy sources try to understand the Bell's problem, written in the right column of this page.
The probable source of stellar energy is proposed here. This result was received in 1998, but it does not accepted yet by the scientific community. The probable cause is hidden in the difficulty of Bell's paradox. In order to understand the energy sources try to understand the Bell's problem, written in the right column of this page.

On the left side of the picture you can see the set of atoms, situated in the inertial frame of reference (IFR), suppose, far in outer space. On the right side of the picture there is the same set of particles, but situated in the non inertial frame of reference, - in or on the surface of a massive bodies, - Sun, Earth, me, you, e.g. in gravity field. Every IFR is in the state of rectilinear uniform motion relatively all others IFR in its locality. But relatively the surface of massive object it will move with the acceleration. From the other hand, particles, resting on the surface of the massive object, will be in the state of constant acceleration relatively any IFR. We can speak unequivocal about distances and time synchronization between particles only in IFR. One can see on the picture the continuous changes of the distances between particles in one host IFR, and how the particles move up to the next host IFR. It is clear from the picture that the process of transition of particle from one host IFR to another host IFR is accompanied by energy transition from space to matter, or space annihilation inside the massive bodies with pumping up the matter of the object by energy. Pay attention on the alteration of values of forces and distances between the particles.
The case of two particles, connected by zero mass spring. On the bottom picture you can see: in green color is the resting spring with two particles with masses m; in red color is the same spring with particles, but which was accelerated to the velocity v; and again in green color is the same spring with the same particles after the process of conjugation of time and length between them, as it follows from the special relativity. We can think that system, painted in red, is in an exited state. System will transfer into non-exited state by radiating a photon, and as a result in the new host inertial reference frame we'll have three particles, - two space-time conjugated massive particles, painted in green, on the picture over the red particles, and one photon.
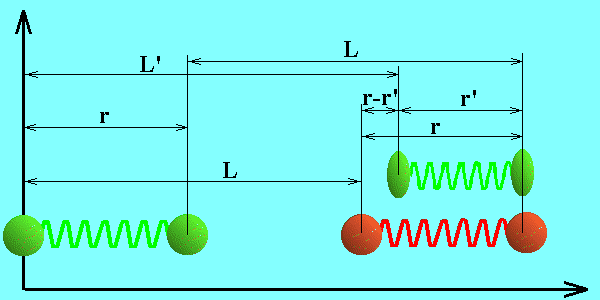
As it follows from special relativity, after the period of acceleration the moving spring must be shorter, in the inertial frame of reference in which that acceleration began. Consequently, one of accelerated particles must pass the bigger distance, and have, correspondingly, more velocity then other particle. In the end of one cycle t=L/v of acceleration, second particle must conjugate its own space-time position by changing virtual photon with another particle, which have in the end of one cycle of acceleration the velocity v. As a result the second particle must cover immediately the distance, equal to reduction of a spring, and consequently its average velocity will be defined as:
v1 = v+(L'-L)/t, (1)
Particles will exchange the virtual photon between them n times during the average period t of space-time conjugation or during the average period of their existence in one host inertial reference frame.
t = 2nr/c = L/v (2)
Here L is the way passed by both particles before the moment of space-time conjugation, L' is the way passed by the second particle, which consists of two parts: L - the way passed before the process of conjugation, and r'- the way, which particle covers in the instant of conjugation. It is clear that:
L'-L = r-r' (3)
r' = r(sqrt(1-v2/c2)) ~ r(1-v2/(2c2)) (4)
v1 = v+rv2/(2c2t) = v+v2/(4nc) (5)
In the end of one cycle accelerator must spent the energy e, which at first goes in maintenance of a "strain in spring", then transfer into difference in the kinetic energy of particles, and, as a result, in transfer to the internal energy of an object, or, in radiation of photon in outer space. If such accelerator is the gravity field, then the source of energy e, spent on space-time conjugation of object's particles is just the space-time of the Universe.
e = mv12/2 - mv2/2 = mv3/(4nc)(1+v/(8nc) ~ mv3/(4nc) (6)
In expression (6) we assumed: 1 + v/8nc ~ 1. Dividing the last expression by t we'll receive elementary auxiliary capacity, which goes not on the accelerating of an object, but on the heating of any accelerated object.
p = e/t = mv3/(4nct). (7)
Substituting in (7) n from (2) and v=gt, we'll receive:
p = mrtg3/(2c2). (8)
Object in the gravity field of another object. In the last expression we substitute g = GM/r02, where, M - total mass of two point body, r0 - radius of an object. As it follows from the bottom picture: r = r0. Supposition: t=t0, t0 = 0.001362 s - universal time interval between successive conjugations, which will be explained a little later. For capacity of probe mass laying on the surface of on object we have:
p = mtG3M3/(2r05c2). (9)
For mass of 1-kg object on the surface of Sun: p(1kg) = 1.084E-04 W. Multiplying this result by mass of the whole Sun we'll receive: p(calculated) = 2.157E+26 W. It is clear that this is very simplified approach, but comparing the result with observable one shows correctness of the selected way: p(observable) = 3.826E+26 W.
The case of spherical object with variable density. Any body, resting in the surface of massive object, will be in the state of acceleration relatively probe point moving free in curved space-time in the same vicinity of massive object, suppose, in free dropping lift. Consequently, free dropping object is in the natural state, in which its inner state is unchangeable. Otherwise surface of a large massive object and any layer of it are in the state of acceleration relatively any inertial reference frame. But in the process of particle pairs conjugation we can see the quantum frame changing, with quantum transition of particle pairs from one host inertial reference frame to the higher energetic level in the next host inertial reference frame. In order to transfer from two point problem to continuous object we'll make calculations dividing the objects on spherical layers and gathering them into a rod as it shown on the bottom picture.
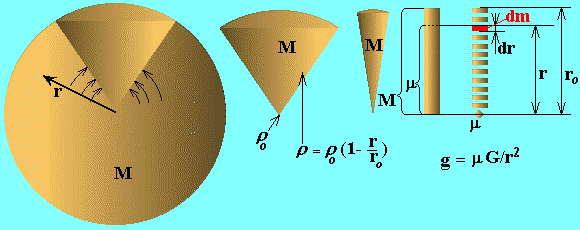
Let's consider the object with linear to the center density r, when dencity is proportional to depth to the star r0-r.
r=r0(1-r/r0). (10)
where r0 is the density in the center of a body, r0 is the radius of a body, r distance to the center. The density of the body can be received from (10) and condition (11), where I - integral from r = 0 to r = r0.
m=I(r4pr2)dr, and m = M. (11)
r0 = 3M/(pr03). (12)
The mass of the object inside the sphere of radius r now can be defined with the help of (10), (12) through total mass of an object:
m=I(r4pr2)dr=12M/(r0^3)*(r3/3-r4/(4r0)), (13)
where I is integral from r=0 to r=r. Acceleration g will be dependent of a distance r to the center of the object:
g = m*G/r2. (14)
After substitution (13) in (14) we'll have:
g = 12MG/(r03)*(r/3-r2/(4r0)). (15)
The sphere with thickness dr at the distance r from the center will have the mass:
dm = rSdr = 4prr2dr. (16)
For elementary power we substitute dm instead of m in (8)
dp = rtg3/(2c2)*(dm). (17)
To receive total power we take the integral I.
p =124M4G3t/(2c2r012)I{(1-r/r0)r3((r/3-r2/(4r0)))3}dr (18)
p =124M4G3t/(2c2r05)*0.000056367
p = 0.5844*M4G3t/(c2r05) (19)
pcalculated = 2.521E26 W
pobservable = 3.826E+26 W
Time interval of space-time conjugation. It is clear that interval of space-time conjugation between particles is not equal to the time that light took to pass the radius of the object. It depends of it, and we must use the second part of expression (6), when we calculate the energy of stars with radius, equal about 100 radiuses of the Sun. But it seems that the conjugation period mostly depends of inner characteristics of space-time, something like tension in solid body. Or it may be deduced through the temperature of vacuum (CMBR), or some other inner characteristics of space-time such as curvature radius of Universe, or Hubble constant, or their derivatives.
In this work were supposed that space-time can be represented as four dimensional lattice. In that lattice N is the quantity of layers situated on every imaginable plane. In every plane (bundle of lines, frame of reference) there are N planes (lines, frames), moving relatively each other and rotating relatively each other. Linear and angular velocity is defined with the help of N. If we divide velocity of light on N we'll have quanta of velocity, which is equal to relative velocity of two IFR:
vmin = c/N. (20)
Kinetic energy of proton (most widespread stable massive particle in the Universe), connected with this quantum velocity, or with this neighbour IFR:
Emin = mvmin2/2. (21)
Frequency:
nmin = c2m/(hN2). (22)
This frequency is the smallest possible frequency. From the other side we know that Hubble constant can be treated as the smallest possible frequency and we can substitute it in (22) in order to define N.
N = sqrt(c2m/(Hh)). (23)
H = 73.28 km/(s*Mpc) = 2.375E(-18) s-1.
N = 3.0909E20
If we multiply number N by H, we also receive frequency:
NH = 734.0 s-1 (20)
In the other sections of this work there was proved that this frequency and time, length, angle, that can be derived from this value, are universal. Then for universal time interval we have:
t0 = 1/(NH) = 0.001362 s (21)
Conclusion. In this section the expression for power, which receives massive object as a result of absorbing material space-time, was at first deduced. Here also, the universal space, time and frequency values were deduced. In other sections they are derived in unexpectedly different ways Gravity, Normalized Units, Universal Units.
p = 0.5844*M4G3t0/(c2r05)
The total luminosity of the Sun is: 3.826 Wt.
The power received by the Sun as a result of space consumption is: 2.521E26
Wt.
The rest of power Sun takes from nuclear sources: 1.305E26 Wt.
Or in percents:
total: 100%
space-consumption: 34.11%
nuclear sources: 65.89%.
Neutrino observations give:
Homestake experiment less then 1/3 or less then 33.3%
Kamiokande around 40%
Galex and SAGE between 50 and 60%.
It seems that the most correct results were received on the Homestake experiment, as based on reactions in chlorine-37 solution. Some others experiments are based on detecting of Cerenkov light emitted by high-velocity charged particles in the water, and it is not excluded that some background events interfere the main source.
It is obvious that such proportion (34% / 66%) of star's energy input is only valid only for the Sun and similar stars. For other stars and planets we'll receive the different proportions. For example, in the case of Jupiter we have space-consumption share more then Jupiter's energy output. That means that Jupiter accumulates nuclear energy and can become the usual star or a nova in a couple billion years.
The dates concerning the neutrino observations one can find in the pages:
This section is the edition of the same-named earlier section, which
is left unchanged as priority of authorship and one can read it by clicking
The upper result was received in 1998.
The 24-th of February 2001 I had received another formula for solar luminosity.
Solar stability
The Solar luminosity can be calculated through: L = GM2H/(4l0), where: M - mass of the stable star, MSun = 1.9891E+30 kg, L- luminosity of a star, LSun = 3.846E+26 W, l0 = ct0 - boundary wave length, or gravity mirror radius, relatively which two halves of the Sun "expand" accordingly to the Hubble law. The change of potential energy of two halves of the Sun in one second is equal to the capacity or luminosity of the Sun.
The formula L = GM2H/(4l0), works excellently; and it proves the correctness of values t0, l0, n0, used everywhere in this website. The time will show which of formulas: 1998 or 2001 is more correct.
Back to index: Space Genetics
Bell's spaceship paradox.
From Wikipedia[2]:
Bell's spaceship paradox is a thought
experiment in special relativity involving accelerated spaceships and strings.
Two spaceships, which are
initially at rest in some common inertial reference frame are connected
by a taut string. At time zero in the common inertial frame, both spaceships
start to accelerate, with a constant proper acceleration g as measured by
an on-board accelerometer. Question: does the string break - i.e. does the
distance between the two spaceships increase?
J.S. Bell explained that the string will break. But if the string will be quite hard, it will pull the spaceships closer to each other, making the accelerations of spaceships different. The cause of attracting force is the mechanical stress, occurring in the string at the process of acceleration. Here is the figure and text from [3].
![]()
Two spaceships A and B joined by a spring. The distance between A and B, observed from the spaceships frame, increases during the acceleration, and then contracts to its original distance L due to the stress of the spring. An observer on the inertial frame S measures the distance as L’, which is Lorentz contracted.
But the contracting string performs the
mechanical work.
- Who spends the energy on that work?
- Accelerator.
- Who will spend the energy, if we change the accelerated frame of reference
by the gravity field?
- Gravitating object, space, gravity, the consumption of the vacuum? Gravity
itself is the consumption of vacuum. As a result, the gravity is the eternal
source of the stellar energy!
- Hardly?
- Yes.
- Even physicists from CERN can not catch it quickly. Read about them in
text from Bell's book:
[1] Three small spaceships, A,
B, and C, drift freely in a region of space remote from other matter, without
rotation and without relative motion, with B and C equidistant from A.
On reception of a signal from A the motors of B and C are
ignited and they accelerate gently. Let ships B and C be identical, and
have identical acceleration programmes. Then (as reckoned by an observer
in A) they will have at every moment the same velocity, and so remain displaced
one from the other by a fixed distance. Suppose that a fragile thread is
tied initially between projections from B and C. If it is just long enough
to span the required distance initially, then as the rockets speed up, it
will become too short, because of its need to Fitzgerald contract, and must
finally break. It must break when, at a sufficiently high velocity, the
artificial prevention of the natural contraction imposes intolerable stress.
Is it really so? This old problem came up for discussion
once in the CERN canteen. A distinguished experimental physicist refused
to accept that the thread would break, and regarded my assertion, that indeed
it would, as a personal misinterpretation of special relativity. We decided
to appeal to the CERN Theory Division for arbitration, and made a (not very
systematic) canvas of opinion in it. There emerged a clear consensus that
the thread would not break!
Of course many people who give this wrong answer at first
get the right answer on further reflection. Usually they feel obliged to
work out how things look to observers B or C. They find that B, for example,
sees C drifting further and further behind, so that a given piece of thread
can no longer span the distance. It is only after working this out, and
perhaps only with a residual feeling of unease, that such people finally
accept a conclusion which is perfectly trivial in terms of A's account of
things, including the Fitzgerald contraction. It is my impression that those
with a more classical education, knowing something of the reasoning of Larmor,
Lorentz, and Poincare, as well as that of Einstein, have stronger and sounder
instincts. I will try to sketch here a simplified version of the Larmor-Lorentz-Poincare
approach that some students might find helpful.
On the left part of the bottom picture there are two
balls, connected be a massless string. v1=v2=0.
String is not stressed.
After the synchronous acceleration balls have equal nonzero velocities
v1=v2=v. Because of synchronous accelerations and
equal velocities at every moment the distance between balls will be the
same as at the start time. But according to the SR theory the length of
a rod, moving with velocity v, must look contracted in the K system.
That is the normal state. Consequently non-contracted (in K system)
string is in fact stretched in the proper system of balls, K'.
Consequently, it is in the stressed state, and we painted it in red
color.

Mechanical forces in the stressed string will move balls closer to each other, and distance between them will look in the K system as contracted. Now the string is again in the normal state, and we painted the system in green color again. To be more precise, we must say, that watches, connected with red balls, showed the equal time readings. That is also contradicts to Minkowski space-time, - their readings must be different. Consequently, before the returning into the normal state, the string was stressed not only in space, but in space-time.
External links:
1.
2.
3.
4.
5.