Квантование скоростей в СТО.
К Теории Струн и Квантовой Гравитации.
Здесь получены удивительные результаты. Красота формул и симметрии настолько впечатляющи, что подход, используемый здесь, не может быть ошибочным. Да, я могу частично заблуждаться в интерпретации результатов, но общий подход является правильным. Здесь мы получаем возможность квантовать пространство-время с помощью СТО.
Квантование пространства-времени НЕ есть его разбиение на элементарные объемы. Под квантованием мы будем понимать представление пространства-времени в виде некоторой решетки, представленной подвижными линиями (или плоскостями), которые мы свяжем с осями подвижных Инерциальных Систем Отсчета (ИСО). Элементарные частицы, а точнее их составные элементы (звенья), некоторое время покоятся на этих линиях-ИСО, а затем мгновенно переходят в соседнюю ИСО, покоятся, переходят, покоятся, переходят... Частицы не живут непрерывно, а материализуются в сериях последовательных пространственно-временных синхронизаций (вспышек). Вспышки происходят после того, как звенья совершат полный обход по всем допустимым ИСО для данного направления.
Квантование выводит нас на сложную геометрию пространства-времени.
Здесь всплывают удивительные связи между квартетом скоростей в СТО
v, vτ, vΨ, vq.
и функциями математики
sin, cos, tg, sh, ch, th...
Кому-то покажется излишним
введение квартета скоростей для описания одного и того же движения,
но пусть он попробует изъять из математики функции
cos, tg, ctg,
описывающие один и тот же поворот.
Пусть выразит все эти лишние функции через
sin
и попробует решать задачи лишь через него. Упростится ли математика от этого?
Две из приведенных скоростей измеряемы, а значит реальны. А какой же из скоростей пользуются частицы, чтобы не нарушить законы сохранения? Какая из скоростей входит в формулы для импульса и энергии для нас, макроскопических наблюдателей? Кое-что мы уже выяснили на предыдущих страницах. Нашли некоторые связи. При этом мы строго пользовались основами теории относительности, стараясь не нарушать её постулаты. Введение квантуемой скорости расширяет саму теорию относительности. Ускоряя частицу, мы доводим её почти до скорости света, и "e;преодолеваем"e; её, но в кавычках. Координатная скорость при этом не свановится сверхсветовой. Частица, по достижению светового предела, улетает за бесконечность справа и одновременно появляется из-за бесконечности слева. При этом оси подвижных координат перехлестываются, меняют направление, как показано на этом gif-анимированном рисунке. Лишь в этом месте мы выходим за пределы общепринятой СТО. У них при достижении скорости света пространственная и временная оси поворачиваются навстречу друг другу и сливаются на повороте 45°, а у нас вот так:

Вот некоторые связи между координатной скоростью v=dx/dt, собственной скоростью vτ=dx/dτ, быстротой vΨ, параметром быстроты Ψ, квантуемой скоростью vq, параметром квантуемой скорости Q, углом поворота подвижной системы координат φ, релятивистским коэффициентом γ.
vt/c = sinQ = sin(vq/c);
vτ/c = tgQ = tg(vq/c);
γ = 1/cosQ= 1/cos(vq/c);
vt/c = thΨ = th(vΨ/c);
vτ/c = shΨ=sh(vΨ/c);
γ = chΨ=ch(vΨ/c);
th(Ψ/2) = tg(Q/2);
thΨ=tgφ;
tg(π/4 + Q) = (tg(π/4 + φ))1/2.
Ускорений оказалось еще больше! Ведь ускорение это производная от скорости по времени, а СТО дает два времени, координатное t и собственное τ.
Караул!
Восемь ускорений для одного и того же ускоренного движения!
Зачем нам все это надо?
Стоять! Проделай выкладки и ты увидишь чудо!
Некоторые ускорения оказываются попарно равны!
Да? Класс!
И второе чудо! Эти пары ускорений образуют лесенку, прогрессию с множителем γ.
Смотри, какая прелесть:
dv/dt = γ0dv/dt; - - - - - - - - - -
dvq/dt = γ1dv/dt; dv/dτ = γ1dv/dt;
dvΨ/dt = γ2dv/dt; dvq/dτ = γ2dv/dt;
dvτ/dt = γ3dv/dt; dvΨ/dτ = γ3dv/dt;
- - - - - - - - - - ; dvτ/dτ = γ4dv/dt.
Эти теснейшие связи между математическими функциями и различными видами скоростей и ускорений для одного и того же движения являются еще одним доказательством истинности СТО.
Собственную скорость vτ=dx/dτ в прошлых разделах мы обозначали буквой b, на рисунке ниже она обозначена vp, от английского proper. В англоязычной Википедии она обозначена буквой w. Её предел - бесконечность. Физический смысл: отношение перемещения к собственному времени движения.
Предел быстроты тоже бесконечность. Используется давно, с рождения СТО.
На квантуемую скорость я вышел в 2007 году.
Пространственно-временное представление электрона и/или другой элементарной частицы.

На этом анимированном рисунке мы видим:
|
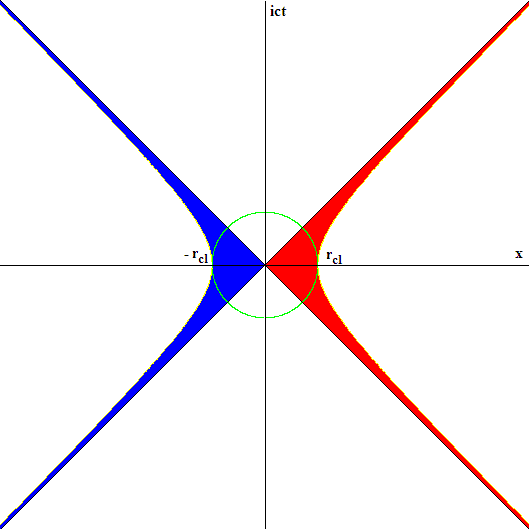
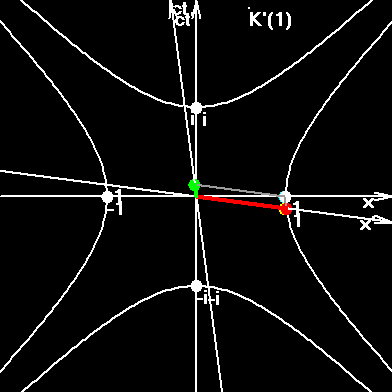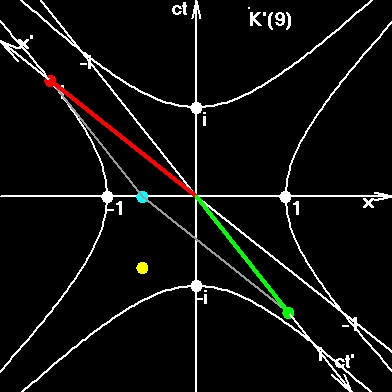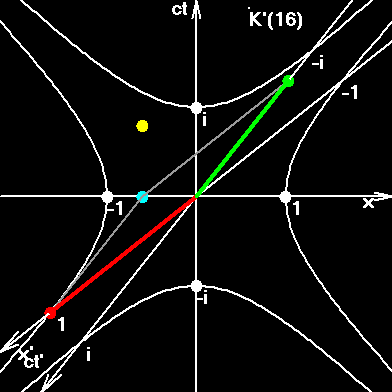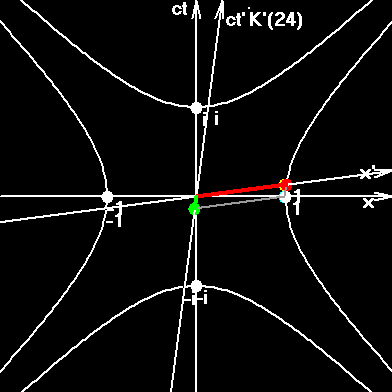
1. Центр элементарной частицы, совпадающий с центром рисунка. Его координаты: (x=0, ict=ictobserver). Вокруг центра - гиперболическое движение. Это движение является открытием No1. Да, оно похоже на гиперболическое движение внутри клина Риндлера, но у Риндлера оно осуществляется вокруг точки (x=0, ict=0). То есть, клин Риндлера "привязан" к моменту старта, а у нас время идет. Кроме того, клин Риндлера направлен вправо, а у нас два клина, движущиеся вперед во времени вместе с точкой x=0, ict=ictobserver.
Вообразите, что центр частицы связан с некоторой точкой, движущейся по правой и левой гиперболам, связан неразрывной идеальной струной. Тогда эта вращающаяся струна окрасит наш рисунок так, как это показано выше. |
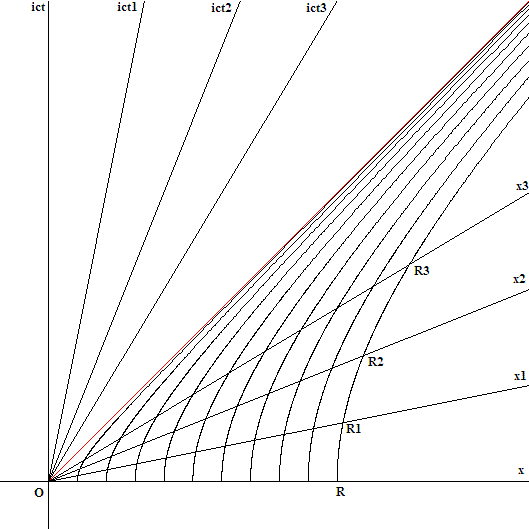
"Будущая" половинка клина Риндлера.
Часть клина Риндлера. События при отрицательных ict не показаны. Главное отличие этого гиперболического движения от нашего в том, что здесь "поворот" идет вокруг x=0, ict=0, а у нас не "поворот", а "вращение" вокруг x=0, ict=ictobserver. Точка x=0, ict=0 является горизонтом событий для всех наблюдателей движущихся по гиперболам, если они ускоряются бесконечно долго. Если же ускорение прекращается, то гипербола переходит в касательную прямую, которая вскоре пересечет световой конус, направленный вверх от x=0, ict=0. |
2. Правая и левая гиперболы представляют собой псевдо-окружность. Её радиусом является красный жирный отрезок (единичный отрезок оси x´ подвижной системы координат), длина которого нам кажется меняющейся. Но это не так. Его длина равна классическому радиусу частицы. Везде! Не забываем, что это комплексная плоскость. Если считать, что rcl=1, то на рисунке мы видим псевдо-окружность единичного радиуса, образованную правой и левой гиперболами. Радиус везде перпендикулярен гиперболам (псевдо-окружности). Открытие No2: Комплексная длина псевдо-окружности бесконечна, но, если для каждого её элемента мы учтем соответствующую релятивистскую поправку, то её длина оказывается мнимой и равной i2πrcl. Верхняя и нижняя гиперболы дают псевдо-окружность действительной длины 2πrcl с мнимым радиусом rcli. Это не просто удивительное совпадение, а какая-то внутренняя симметрия между окружностью и псевдоокружностью. Поэтому мы вводим еще одну движущуюся точку. Это желтая точка, вращающаяся по окружности.
Длина дуги, которую нарисует желтая точка, с точностью до множителя i равна релятивистской длине дуги пройденной концом красного отрезка, движущегося по "право-левой гиперболе". |
Временная развертка нашего гиперболического движения. (Один из видов.)
|
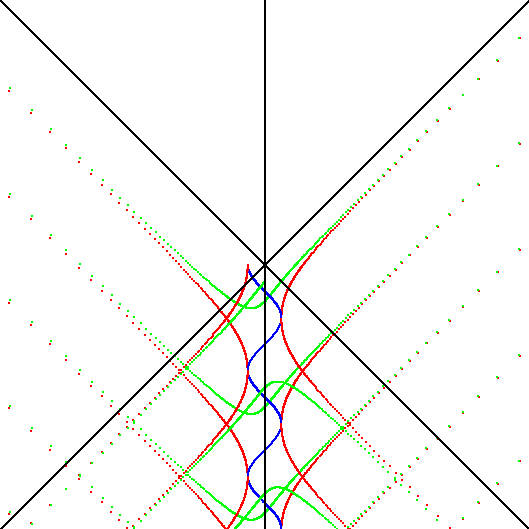
3. Жирный красный отрезок является единичным отрезком, пробегающим оси подвижных ИСО, x´. Зеленый отрезок соответствует временным осям подвижных ИСО, ict. В СТО утверждается, что скорость света является пределом, недостижимым для частиц, имеющих массу покоя. Поэтому пределом поворота осей подвижных ИСО был угол π/4. Открытие No3: Введение квантовой скорости показывает, что пределом координатной скорости действительно является скорость света. Но частицы "проскакивают" её так, что квантуемая скорость продолжает свой рост, оси меняют направление на противоположное, угол поворота осей (φ) на анимированном рисунке совершает скачек на π радиан. В этом ничего удивительного нет! При переходе от предельно возможной квантуемой скорости в первом квадранте π/2-δQ к следующему значению во втором квадранте π/2+δQ, квантуемая скорость возрастет, а координатная будет той же, поскольку v = c·sin(π/2-δQ)=c·sin(π/2+δQ). |
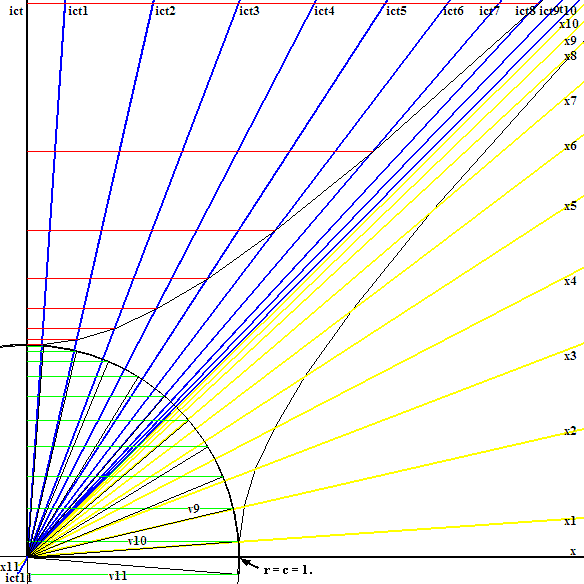
Набор из 10 скоростей. Координатные скорости - зеленые отрезки. Квантуемая скорость - соответствующие дуги на окружности. Быстрота - соответствующие дуги на гиперболе. Собственные скорости - соответствующие красные отрезки. Обратите внимание, как осуществляется квантовый переход между десятой и одиннадцатой скоростью... как "преодолевается" скорость света. |
| Еще раз вернемся к нашему анимированному рисунку. СТО не является квантовой теорией. В настоящей работе предполагается, что скорость, с которой может двигаться элементарная частица, не может иметь непрерывный ряд значений. Скорость может меняться малыми порциями. Здесь всего лишь пара десятков кадров, где показан переход из одной ИСО в другую ИСО, а нам кажется, что это ускоренное движение непрерывно. В действительности, движение на микроуровне тоже может представлять собой совокупность кадров, но количество этих кадров будет на много порядков больше. Далее мы попытаемся разбить скорость на огромное число допустимых скоростей. Частицы могут двигаться с этими скоростями, но промежуточных скоростей нет. |
|
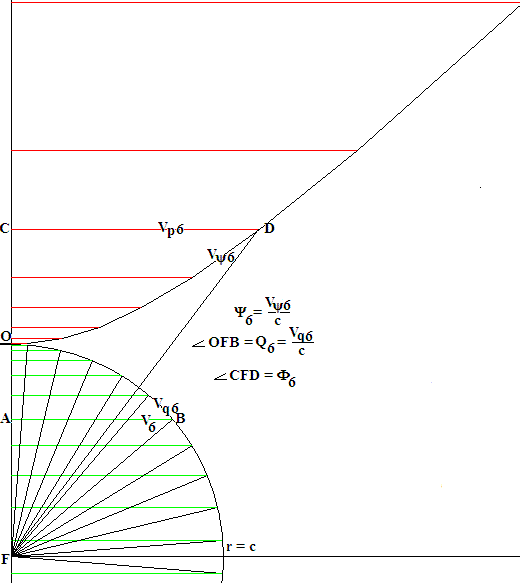
| Вот набор из десяти скоростей, которые мы "переложим" на оси подвижных ИСО.
Сравним по рисунку длины квартета скорости 6. Самый короткий отрезок - координатная скорость v6. Очевидно, что длина vq6 будет чуть-чуть больше. Дальше идет комплексная длина дуги vΨ6, поскольку это именно её укорачивали релятивистским множителем гамма, чтобы получить дугу vq6. Самым длинным в квартете будет отрезок собственной скорости, обозначенный как vp6. Визуально нам кажется, что дуга vΨ6 длиннее отрезка vp6, но нужно иметь ввиду, что каждый элемент дуги есть корень из суммы квадратов dx и d(ict), а i2=-1, превратит сумму в разность. |
Пространственные координатные оси подвижных систем координат (линии
одновременных событий) окрашены желтым цветом. Временн´ые - синим.
Обратите внимание на переход v9, v10, v11 (зеленые отрезки, соответствующие координатной скорости). Соответствующие дуги квантуемой скорости преодолевают угол π/2, а угол поворота осей приближается к π>/4 и... Куда должны быть направлены оси одиннадцатой системы? Правильно! В третий квадрант. На этом рисунке они показаны в еле заметном уменьшенном виде. |
| На самом деле число N давно вычислено в этой работе с
достаточно большой точность. Квадрат этого числа с точностью до числового коэффициента равно числу Дирака и связывает отношение гравитационных и электромагнитных взаимодействий, а также космологические величины
с атомными. Вне всякого сомнения, Дирак ухватился за большие числа с целью
получить структуру пространства-времени на микроуровне (т.е. квантовать
пространство-время), но в то время начала набирать обороты ложная религиозная
космологическая модель, в которой Вселенная расширяется, а соответственно -
констант нет, числа меняются.
В настоящей работе гипотеза Большого Взрыва считается бредятиной. Наша константа Хаббла не является параметром расширения Вселенной, а характеризует её угловую скорость в четырехмерном вращении. Время одного полного оборота Вселенной не является её возрастом.
|
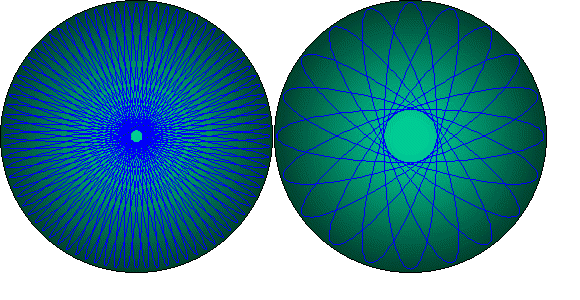
Слева мы видим n поворотов квадрата на угол 2π/n и попадаем с классического радиуса частицы на планковские величины (длина одного ребра многоугольника, которым можно очертить данный рисунок). Этот же многоугольник мы можем найти в центре рисунка ниже. При этом, для того чтобы попасть с размеров электрона (протона) на планковские величины работает число N, а чтобы попасть на длину большой окружности Вселенной - N2.
Псевдоокружность квантуемой скорости делим на 4N (т.к. имеется 4 квадранта). Соответственно, полный набор должен представлять 4N подвижных ИСО. |
Пачка ИСО - это математический трюк,
|
Выход на планковские величины. |
| Представьте себе, что Вы уснули в каюте океанского лайнера. Иллюминаторы зашторены. Никакой качки. Вопрос: движется ли Ваш лайнер, или
же стоит у причала? Согласно СТО Эйнштейна и согласно нашему накопленному опыту, мы не можем отличить покой от равномерного прямолинейного движения. А значит ИСО, связанная с бухтой, и любая другая, движущаяся равномерно и прямолинейно равноправны. Но конечно ли количество таких ИСО? Согласно ОТО Эйнштейна ощущения пассажира, свободно падающего вместе с кабиной оборвавшегося лифта, а также его свободное движение без ускорения в межзвездном пространстве, почти неотличимы. За исключением финала и некоторой кривизны пространства-времени. Переход в n-ую ИСО, и очень резкий, минуя огромное количество других ИСО, произойдет лишь в момент падения лифта на землю. О количестве ИСО, которые почти мгновенно перескочил бедолага в лифте, можно будет судить по состоянию его скелета… Монотонный переход из одной ИСО в другую ИСО происходит в случае, когда человек ускоряется в ракете в межзвездном пространстве, к примеру с ускорением g=9,8м/c2. Точно такие же ощущения он чувствует стоя в лифте, покоящемся на поверхности Земли. Если человека там закрыли, дали крепко уснуть, то он, проснувшись, не сможет отличить, а где же он сегодня: ускоряется в ракете с ускорением a=9,8м/c2, или же покоится в поле тяжести Земли, переходя монотонно из одной ИСО в другую ИСО, с ускорением g=9,8м/c2. Однако, рассуждения о поведении макрообъекта и микрообъекта в плане количества допустимых ИСО будут различными. Элементарная частица, имеющая массу покоя, не может иметь ни нулевую скорость, ни скорость, равную скорости света. Макроскопический объект может иметь скорость равную нулю, поскольку он состоит из множества элементарных частиц. Пускай для наглядности он состоит из двух элементарных частиц. Тогда если одна из частиц движется в одном направлении с минимально возможной скоростью, а другая - в другом направлении с такой же скоростью, то скорость этого составного тела будет равной нулю. Кроме того, в этой работе предполагается, что элементарная частица сама по себе является составной. По всей вероятности, она имеет от одного до четырёх элементов, которые мы именуем звеньями пространственно-временной решетки. Анализ работ других авторов показывает, что наши звенья пространственно-временной решетки, пробегающие замкнутую совокупность ИСО, и опоясывающие всю Вселенную, напоминают струны, замкнутые образования в многомерном пространстве. Но авторам струнных теорий, стоящим на позициях догмы Большого Взрыва не позавидуешь - их пространство расползается и у них нет космологических констант: угловой скорости света, H, времени одного полного 4-d оборота Вселенной, T, большого числа Дирака, D=N2, точного значения гравитационной постоянной G, которая получается в нашей модели. Звенья, или дефекты пространственно-временной решетки вращаются по почти замкнутым окружностям, спиралям со скоростью c и "сталкиваются" (стыкуются, синхронизируются...) в некоторых точках, лежащих на мировой линии элементарной частицы. Шаг спирали говорит нам о скорости частицы, v. Моменты "столкновения" дефектов решетки являются актами материализации элементарной частицы. Элементарная частица не существует в моменты времени между микро-материализациями, или для частицы не существует времени между микро-материализациями. Если какое-то звено пришло с опозданием/опережением к месту приходов других звеньев частица, то частица совершает поворот в пространстве-времени, то есть, приобретает элементарный акт ускорения в соответствующем направлении. Так осуществляются электромагнитные и ядерные взаимодействия. Кроме микроскопических синхронизаций (слабая, сильная, электромагнитная) существует также макроскопическая синхронизация, происходящая с частотой порядка 734 Гц, и добавляющая этим частицам еще одно звено - гравитационное, ответственное за существование таких макроскопических объектов, как камень, ячейки Бернара в атмосферах планет, ячейки на поверхности Солнца. Время на границах таких объектов максимально синхронизировано. Время между точками разных объектов может дрейфовать. Акты пространственно-временной синхронизации между частями объекта приводит к нагреву объекта (к энерговыделению в недрах звезд, Солнца). В сущности это и есть Квантовая Гравитация: квантованный процесс, осуществляющий помимо силового воздействия еще и накачку недр планет и звезд энергией. От описания поведения элементарных частиц в пространстве-времени можно перейти к описанию структуры пространства-времени. Как его структурировать? Вероятно, для каждого типа элементарных частиц эта структура выглядит несколько по-разному. С учетом вида взаимодействия можно рассматривать отдельные "сечения" структуры пространства-времени. А полученные результаты можно попытаться перенести на другие сечения. Сравнивая электромагнитные взаимодействия с гравитационными, мы получаем классический радиус частицы. Действительно, мы получаем его, приравнивая энергию покоя частицы (E = mc2, где: m - инертность, являющаяся характеристикой гравитационных взаимодействий) и энергию электрического поля, полагая, что вся масса частицы сосредоточена в форме поля, (а поле есть характеристика электромагнитных взаимодействий). На сравнении этих взаимодействий мы также получили некоторые соотношения, и, прежде всего, большое квантовое число N. Используя формулу mc2=hc/(2πr), мы получим комптоновский радиус, который в 1/α раз больше классического. По предположению в этой работе, комптоновский радиус определяет расстояния, на которых могут находиться одновременные параллельные линии; а на классическом радиусе мы можем работать абсолютно точно относительно некоторой точки, но неопределенность положения этой точки в пространстве и времени определяется комптоновским радиусом. О фундаментальности классического радиуса здесь сказано в связи с тем, что именно через этот радиус удалось выйти на квантуемую скорость. А используя связи между разными видами скоростей, мы можем найти полные наборы допустимых скоростей. В настоящей работе показаны следующие виды скоростей: координатная скорость v=dx/dt, собственная скорость vτ=dx/dτ, быстрота vΨ=c·Arth(v/c), квантуемая скорость vq=c·Arcsin(v/c). На странице Квантуемая скорость и Модель элементарной частицы показаны некоторые свойства квантуемой скорости. Сначала в рассуждениях мы используем некоторое приспособление, которое мы назовем костыль, как противоположный электрический заряд в центре исследуемой частицы. Потом мы избавляемся от него путем эквивалентной замены действия электрического поля, на собственное магнитное поле, создаваемого исследуемой частицей. Ну и наконец, учитывая, что сильные взаимодействия в 137 раз сильнее электромагнитных, мы распространим наши рассуждения на строение протонов и нейтронов. Квантуемая скорость была получена с помощью мысленного опыта, заключающегося в том, что если элементарный заряд падает на противоположный заряд, закрепленный в точке с координатой x=0, то его образ монотонно пробегает все точки правой и левой гиперболы. При делении каждого элемента гипербол на релятивистский коэффициент (chΨ = γ) две гиперболы превращаются в окружность радиуса rcl. При этом образ частицы движется по этой псевдо-окружности равномерно. Длина дуги, измеренная от точки пересечения с осью x до нижней точки окружности, есть величина -r·iπ/2, а до верхней точки r·iπ/2. Разделив эти значения на r·i, мы получим фазу колебаний Q, и она же есть параметр квантуемой скорости, Q. Умножая этот параметр на скорость света, получаем квантуемую скорость vq=c·Q. Действительно, длину четверти окружности дает нам половина гиперболы при делении каждого её элемента на релятивистский коэффициент chΨ, и последующего взятия интеграла с пределами интегрирования от нуля до плюс бесконечности. Q(1/4) = 0∫+∞dΨ / chΨ = π/2. Вставка от 15.05.2018. Изобрести что-то новое и верное почти невозможно. Оказывается, величина, которую я обозначил буквой Q, уже давно изобретена. Только в нашем случае это параметр квантуемой скорости, а у других это называлось "гиперболическая амплитуда", "функция Гудермана", "гудерманиан". Она связывает тригонометрические и гиперболические функции без привлечения комплексных чисел. Обозначают и определяют её следующим образом: gd(x) = 0∫x dt / ch t. Перепишем это в наших обозначениях: Q = 0∫Ψ dΨ / chΨ. А также позаимствуем у наших предшественников одно удивительно красивое соотношение, которое мы запишем в наших обозначениях: Ψ = 0∫Q dQ / cosQ. Заметим, что это не просто еще одно красивое симметричное соотношение между гиперболическими и тригонометрическими функциями, а существенно больше: Эти функции связывают заряженные частицы и их поля в одну многогранную сущность. Другими словами, электрон - это не просто волна, или частица, а скорее и то, и другое, а еще и поле, и элемент пространства - временное вместилище для других частиц. |
Полный набор подвижных ИСО составляет 4N
систем. Половина из них ориентирована в положительном направлении
центральной ИСО и их скорости лежат в пределах (-с, с), половина - в
отрицательном и с таким же диапазоном (-с, с).
Для того чтобы получить полный набор положительных значений скоростей мы должны разделить четверть псевдоокружности (верхнюю половину правой гиперболы) на N дуг равной релятивистской длины. Таким образом мы получим полный набор квантуемой скорости. Зная этот набор, мы можем получить наборы других типов скорости (координатной vt, собственной vτ, быстроты vΨ). Число N это большое квантовое число. В настоящей работе оно предполагается равным 3,09·1020. Кроме того, необходимо учесть, что, превращая окружность в многоугольник, мы должны учесть, что значение минимальной скорости не должно быть равно нулю, а значение максимальной скорости не должно быть равно в точности "с". Этого мы можем добиться, строя правильный 4N-угольник так, чтобы оси x и ict пересекались срединами ребер получаемого 4N-угольника. Тогда минимальное значение параметра квантуемой скорости будет определяться интегралом не от полного ребра, а от его половинки. Qmin = Q1 = o∫ψ1 dΨ / chΨ = (π/2) / N /2 = π / 4N. Следующее значение параметра квантуемой скорости отстоит на целое ребро 4N-угольника. Q2 = o∫ψ2 dΨ / chΨ = π / 4N + π / 2N = 3π / 4N. Следующее допустимое значение: Q3 = o∫ψ3 dΨ / chΨ = 5π / 4N. Очевидно, что n-e допустимое значение параметра квантуемой скорости будет определяться по формуле: Qn = o∫ψn dΨ / chΨ = (2n-1)·π / 4N. Максимальное значение параметра квантуемой скорости будет при n=N: Qmax = (2N -1)·π / (4N) = π / 2 - π / 4N. Перейдем от параметра квантуемой скорости к параметру быстроты, пользуясь соотношением tg(Q/2)= th(Ψ/2). Ψn = 2Arth(tg(Qn/2)) = ln((1+tg(Qn/2))/(1-tg(Qn/2))) = ln(tg(π/4 + Qn/2)) Ψmin = π / 4N, Ψmax = ln(8N/π). Запишем выражения для допустимых значений координатной скорости, пользуясь соотношением v=c·sinQ. vn = c·sinQn= c·sin((2n-1)·π / 4N). vmin = c·π / 4N. vmax /c = sinQmax = sin(π
/ 2 - π / 4N) = cos(π
/ 4N) = Запишем выражения для допустимых значений собственной скорости, пользуясь соотношением vτ=c·tgQ. vτ,n = c·tgQn = c·tg((2n-1)·π / 4N). vτ,min = c·tg(π / 2N) = c·π / 4N. vτ,max
/c = shΨmax = sh(ln(8N/π)),
Arsh(vτ,max /c) = ln(8N/π),
Запишем выражения для допустимых значений релятивистского коэффициента γ, пользуясь соотношением γ = 1/cosQ = chΨ. γn = 1/cosQn = 1/cos((2n-1)·π / 4N). γmin = 1/cosQmin = 1/cos(π / 4N) = 1 / (1 - π2 / 16N2) = 1 + π2 / 16N2. γmax = 1/cosQmax = 1/cos(π/2 - π / 4N) = 1/sin(π / 4N) = 4N/π. Итак, максимальное значение релятивистского коэффициента γmax равно 4N/π. О чем это говорит. Каким станет классический радиус электрона, если он будет двигаться с максимально возможной скоростью? Для ответа на этот вопрос разделим rcl = e2 / (4πε0mc2) на 4N/π. Величина N используется повсеместно в нашей работе, и N = (απ / df)1/2, где df есть отношение сил для электрона, df=4πε0Gm2/e2. rcl' = rcl / (4N/π), rcl' = (e2 / (4πε0mc2)) / (4(&alphaπ / df)1/2/π), rcl' = (hG / 32c3)1/2. Полученная величина с точностью до коэффициента равна планковской длине, которую обычно записывают в виде rPl = (hG / 2πc3)1/2. Можно сказать, что мы ошиблись на числовой коэффициент. Но планковские величины никто никогда не наблюдал. Это лишь простой набор констант, дающий естественную длину на микроуровне. Поэтому, полученная нами формула не менее верна. Аналогично можно показать, что релятивистская масса электрона, движущегося с максимально возможной скоростью, равна "нашей" планковской массе: mr = m0 · 4N/π. mr = (α/π)·(8hc / G)1/2. Обычно планковскую массу записывают в форме: mPl = (hc / 2πG)1/2. Здесь мы тоже получаем отличие от общепринятой формулы в численный коэффициент. Не исключено, что в полученные нами формулы должно входить некоторое другое большое квантовое число, тем более, что наша N получена, прежде всего, через космологические параметры и параметры протона. Аналогичные рассуждения, с получением классического радиуса, и описанием движения по гиперболам, можно было бы провести и для самого протона, но, к настоящему времени у меня сложилось впечатление, что "сильное" звено протона вращается в плоскости (y,z), а его электромагнитное звено (позитрон) вращается в плоскости (x,ict), точно также, как и для электрона, но в противоположную сторону. Логично предположить, что "сильное" звено вращается по окружности в mpr/mel раз меньше чем электромагнитное. Это как раз то колечко, сквозь которое пролетает электрон в своем колебательном движении вдоль оси x. Возвращаясь к полученному результату (γmax=4N/π), можно заметить еще одну деталь. Если длина большой окружности Вселенной определяется по формуле X = Nλ0 = N2λpr, где λ0-граничная длина волны между фотоном и гравитоном, λpr - комптоновская длина волны протона, то Вселенная относительно электрона, движущегося с максимально возможной скоростью, будет сокращена в 4N/π раз. Разделив X=Nλ0 на γmax=4N/π, мы получим λ0·π/4. А это и есть длина "гравитационного звена", которое частицы пролетает её за время t = (λ0·π/4) / vq.max = (λ0·π/4) / vq.max = (λ0·π/2) / (cQmax) = λ0/c = τ0. Величина τ0 есть граничный период между электромагнитными и гравитационными колебаниями, то есть между гравитонами и фотонами. |
Вперёд: Квантуемая скорость и Модели элементарных частиц.
Назад: Разные формы записи преобразования координат.
К оглавлению раздела Некоторые вопросы СТО.
К другим разделам Космической Генетики.
Моя VB-программа "Электрон". EXE-файл..
Страница создана 29 мая 2007 г.
Отредактирована февраль 2016, май 2018.