4-d вращение.
Прелесть!!!
Но давайте тормознемся и начнем из очень, очень, ну очень вкусных, сфероподобных, слегка грязных... но для иллюстрации сойдёт.

Яйца не являются 4-мерными объектами. Они же куриные. Трёхмерные. Имеют длину, ширну и высоту. А сколько яйц можно уложить вплотную друг к другу вокруг одного центрального? Пусть они будут идеально сферические.
Да!
6!
Конечно-же, в 2d пространстве вы можете уложить точно 6 идеальных кругов без зазоров и перекрытий вокруг центрального круга.
В трехмерном пространстве мы может построить живописные трехмерные упорядоченные конструкции.
Как видим, в 3d пространстве одно центральное изумрудное яйцо мы можем обложить аж 12-ю яйцами абсолютно идеального радиуса.

Вы видите, что на тарелке лежит одно изумрудное яйцо, а с боков и снизу его целуют 9 белых яиц.
А где же еще три яйца? - спросите вы.
А вы довообразите их снизу. Потренируйтесь дома взять 13 яиц из холодильника и удержать их двумя руками.
И, Осторожно! Не напрягайте мозги и не сильно сдавливайте яйца. Мозги могут взорваться, а яйца - треснуть. Цену вашему мозгу я не знаю, но за разбитые яйца ваши родители могут...
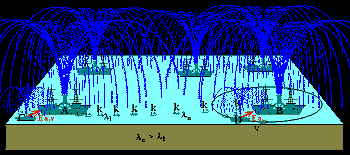
В 4d пространстве один четырехмерный шар вплотную можно обложить 24-мя шарами такого же радиуса.
На gif-анимированном рисунке ниже показан пример наиболее плотной упаковки
шаров в 4-мерном пространстве. Для удобства шары показаны с уменьшенным
радиусом, чтобы мы могли видеть шары, находящиеся дальше. Четвертая координата
ассоциирована с цветом. Мы находимся по цветовой координате в точке "зеленый".
Образно говоря, вы сидите на стуле. Вы зеленый по цветовой координате. На том же стуле одновременно может сидеть и ваша жена, если она красная в четвертом измерении и вы при этом друг другу не мешаете. Ваша любовница тоже может сидеть на том же стуле, если она синяя в 4d. В принципе ваш стул может вместить сотни ваших любовниц, если вы развратный мэн и если все ваши женщины разноцветны.
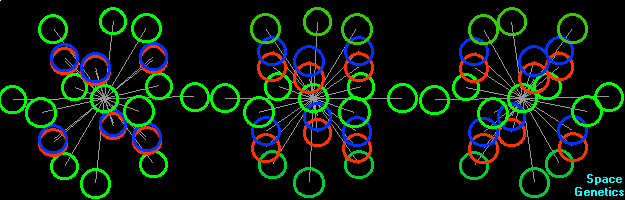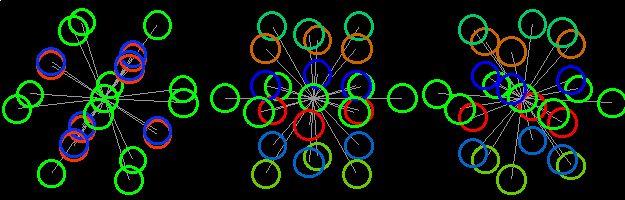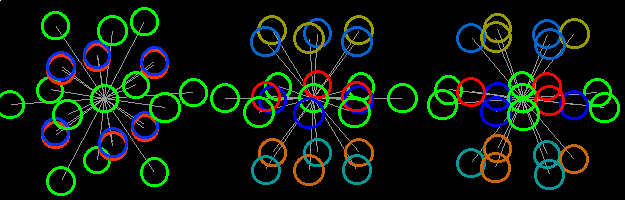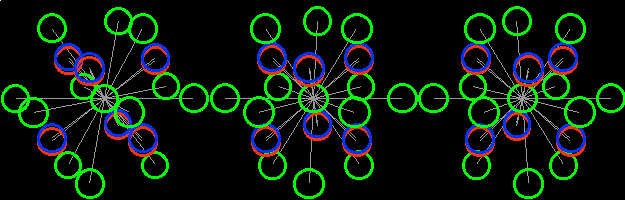
Так, давайте вернемся к нашим 4d шарам. Вращение происходит следующим образом:
Левая группа шаров вращается в горизонтальной плоскости xy.
Средняя группа шаров вращается в вертикально-цветовой плоскости zq.
Правая группа шаров вращается в обеих плоскостях.

Оуу!!! Ничего себе! Четырехмерное вращение обладает некоторыми замечательными свойствами.
1. Правая вещь постепенно сжимается, становится плоской, потом становится левой...
Смотри! Вот это чертовщина! Правый башмак превратился в левый, потом в правый, потом опять в левый...


Образно говоря, для того чтобы сделать из правого ботинка левый, вы должны повернуть его в плоскости zs на π радиан вокруг оси-плоскости xy. Но если вы прогуливали уроки геометрии, и попытаетесь повернуть свой правый ботинок в плоскости xz вокруг оси y, то вы сможете увидеть лишь грязь на подошве вашего башмака.


Мой юный друг ты всё перепутал. Надо было поворачивать в плоскости, содержащей четвёртую координату, которую мы здесь отождествили с цветом.

2. А тем, кто усвоил повороты-превращения, предложим второе замечательное свойство 4d вращения. Эти 24 шара могут быть приведены в два взаимно перпендикулярных вращения одновременно. При этом конфигурация шаров меняется, но расстояния у оболочечных шаров до цетра остается тем же, равным двум радиусам шаров. Зазоров между шарами как не было, так и нет. Но на этом рисунке мы видим зазоры. Это сделано для удобства, чтобы видеть задние шары. На рисунке шары заменены окружностями меньшего радиуса. На самом деле при наиболее плотной упаковке вточности одинаковых шаров вокруг центрального шара будет 24 шара. Без зазоров в любой момент вращения. Видимая конфигурация меняется. Зазоры остаются нулевыми.
Давайте вернемся к нашим 4d шарам.

Ну и где эти шары? Какие у них координаты?
OK. Я хоть и не математик, но нашел их. Потратил, конечно же массу времени и сил. Потом сделал проверку. Все срослось. Поэтому не парьте мозги. Даю вам готовое решение.
Это решение есть один набор координат 24 шаров из непрерывного бесконечного множества таких наборов, при наиболее плотной упаковке.
Первые шесть точек дают упаковку в 2d плоскости.
Первые 12 дают упаковку в 3d.
Ну а все 24 - упаковка в 4d.
Центральный шар занумеруем циферкой 0. Его координаты - (0, 0, 0, 0).
Сферы оболочки нумеруем цифрами-именами
1, 2, 3... 24.
Координаты записаны в круглых скобках.
В квадратных скобках записаны номера-имена тех шаров оболочки, с которыми контактирует данный оболочечный шар.
1 (1, 0, 0, 0) [2,6,7,10,13,16,19,22]
2 (1/2, -√3/2, 0, 0) [1,3,7,12,15,16,21,22]
3 (-1/2, -√3/2, 0, 0) [2,4,8,12,15,17,21,23]
4 (-1, 0, 0, 0) [3,5,8,11,14,17,20,23]
5 (-1/2, √3/2, 0, 0) [4,6,9,11,14,18,20,24]
6 (1/2, √3/2, 0, 0) [1,5,9,10,13,18,19,24]
7 (1/2, -1/(2·√3), √2/√3, 0) [1,2,8,9,13,15,19,21]
8 (-1/2, -1/(2·√3), √2/√3, 0) [3,4,7,9,14,15,20,21]
9 (0, 1/√3, √2/√3, 0) [5,6,7,8,13,14,19,20]
10 (1/2, 1/(2·√3), -√2/√3, 0) [1,6,11,12,16,18,22,24]
11 (-1/2, 1/(2·√3), -√2/√3, 0) [4,5,10,12,17,18,23,24]
12 (0, -1/√3, -√2/√3, 0) [2,3,10,11,16,17,22,23]
13 (1/2, 1/(2·√3), 1/√6, 1/√2) [1,6,7,9,14,15,16,18]
14 (-1/2, 1/(2·√3), 1/√6, 1/√2) [4,5,8,9,13,15,17,18]
15 (0, -1/√3, 1/√6, 1/√2) [2,3,7,8,13,14,16,17]
16 (1/2, -1/(2·√3), -1/√6, 1/√2) [1,2,10,12,13,15,18]
17 (-1/2, -1/(2·√3), -1/√6, 1/√2) [3,4,11,12,14,15,16,18]
18 (0, 1/√3, -1/√6, 1/√2) [5,6,10,11,13,14,16,17]
19 (1/2, 1/(2·√3), 1/√6, -1/√2) [1,6,7,9,20,21,22,24]
20 (-1/2, 1/(2·√3), 1/√6, -1/√2) [4,5,8,9,19,21,23,24]
21 (0, -1/√3, 1/√6, -1/√2) [2,3,7,8,19,20,22,23]
22 (1/2, -1/(2·√3), -1/√6, -1/√2) [1,2,10,12,19,21,23,24]
23 (-1/2, -1/(2·√3), -1/√6, -1/√2) [3,4,11,12,20,21,22,24]
24 (0, 1/√3, -1/√6, -1/√2) [5,6,10,11,19,20,22,23]
Далее замечаем, что, имея эти координаты, мы можем совершить повороты в плоскостях xy и zt. Для этого выражаем координаты через синусы и косинусы некоторых углов. Поворот на произвольный угол мы можем заменить на постоянное вращение.
Вот примерный кусок программы, с помощью которой, мы можем задать координаты точек через интервалы времени, по истечению которых, совершается поворот на π/30 радиан в обеих плоскостях.
fi = pi / 3
M = Sqr(2 / 3)
For t = 0 To 20
psi = 0 + t * pi / 30 'вращение в плоскости zc
hi = 0 + t * pi / 30 'вращение в плоскости xy
a(0) = 0 'координаты центрального шара
b(0) = 0
c(0) = 0
d(0) = 0
For i = 1 To 6 'координаты шаров 1, 2,.. 6.
a(i) = Cos(-fi * (i - 1) + hi)
b(i) = Sin(-fi * (i - 1) + hi)
c(i) = 0
d(i) = 0
Next
For i = 7 To 9
a(i) = Cos(-fi / 2 - 2 * fi * (i - 7) + hi) / Sqr(3)
b(i) = Sin(-fi / 2 - 2 * fi * (i - 7) + hi) / Sqr(3)
c(i) = M * Cos(psi)
d(i) = M * Sin(psi)
Next
For i = 10 To 12
a(i) = Cos(fi / 2 + 2 * fi * (i - 10) + hi) / Sqr(3)
b(i) = Sin(fi / 2 + 2 * fi * (i - 10) + hi) / Sqr(3)
c(i) = M * Cos(psi + pi)
d(i) = M * Sin(psi + pi)
Next
For i = 13 To 15
a(i) = -Cos(-fi / 2 - 2 * fi * (i - 13) + hi) / Sqr(3)
b(i) = -Sin(-fi / 2 - 2 * fi * (i - 13) + hi) / Sqr(3)
c(i) = M * Cos(psi + pi / 3)
d(i) = M * Sin(psi + pi / 3)
Next
For i = 16 To 18
a(i) = Cos(-fi / 2 - 2 * fi * (i - 16) + hi) / Sqr(3)
b(i) = Sin(-fi / 2 - 2 * fi * (i - 16) + hi) / Sqr(3)
c(i) = M * Cos(psi + pi + pi / 3)
d(i) = M * Sin(psi + pi + pi / 3)
Next
For i = 19 To 21
a(i) = a(i - 6)
b(i) = b(i - 6)
c(i) = M * Cos(psi + pi + 2 * pi / 3)
d(i) = M * Sin(psi + pi + 2 * pi / 3)
Next
For i = 22 To 24
a(i) = a(i - 6)
b(i) = b(i - 6)
c(i) = M * Cos(psi + 2 * pi / 3)
d(i) = M * Sin(psi + 2 * pi / 3)
Next
В любой момент времени расстояние от каждого оболочечного шара до центрального
шара равно единице. В любой момент времени расстояние между любыми двумя
оболочечными шарами равно или больше единицы.
Раньше я предполагал, что в n-мерном пространстве вокруг шара радиуса r, можно упаковать m = 3·2n-1 шаров такого же радиуса. Оказалось что эта формула справедлива лишь для размерностей 2, 3 и 4.
Четырехмерное вращение Вселенной.
Если Вселенная замкнута, то она обязана вращаться. Все её точки обязаны двигаться с одной и той же 4-скоростью, и с одной и той же угловой скоростью. И этот рисунок нужно усложнять.

Обычный мячик Вы так не раскрутите. Точки мячика возле оси вращения движутся с меньшей линейной скоростью, чем экваториальные точки.
Но замкнутая Вселенная оказывается идеальной в отношении вращения. Она оказывается пространственно однородной и изотропной. Как такое может быть? Ведь на рисунке слева видна явная анизотропия, - мы видим две оси вращения.
Этот рисунок, действительно, помогает нам понять четырехмерное вращение трехмерной неевклидовой гиперсферы x2+y2+z2+q2=r2, погруженной в Евклидово четырехмерное пространство. Но в этом уравнении фигурирует пространственная координата q, которую на рисунке мы отождествили с цветом.
Давайте заменим её на временную координату t, помноженную на скорость света, чтобы получить метры, и на мнимую единичку i, ведь пространство-время псевдоевклидово. То есть получаем уравнение: x2+y2+z2+(ict)2=r2, псевдоевклидовой гиперсферы.
Вы могли бы посмотреть на это вращение в плоскости (x,ict), открыв мою программу, но сейчас файлы с расширением exe не загружаются на сайт. В ближайшее время я попробую сделать анимированный gif-рисунок.
Отметим, что там вращается электрон, пробегая за свое классическое время правую и левую гиперболу. Там же вы видите как "тень" электрона рисует окружность. Эту окружность мы получим, если разделим каждый элемент гиперболы на соответствующий релятивистский множитель, и просуммируем их. В результате получаем 2πri. Это наводит на мысль что пседвоокружность в замкнутой Вселенной превращается в квазизамкнутую окружность не только для электрона, но и для всех частиц во Вселенной, включая галактики.
Итак, куда же девается асимметрия? Для этого вспомним что квадрат 4-скорости (vγ, icγ) в специальной теории относительности является инвариантом и он равен -c2. Для любого тела! Пространственная часть четырехскорости для покоящегося тела равна нулю, а временная дает нам скорость света.
Берем любую точку замкнутой вращающейся Вселенной. У любой точки существует две оси-плоскости. На одной оси она находится, а другая ось расположена перпендикулярно. Обе являются окружностями. Ось, на которой находится рассматриваемая частица содержит координату времени и любую другую, пространственную. Пускай это будет (z,ict). Эта ось движется со скоростью с. Для нашей исследуемой частицы эта скорость будет чисто временной, поскольку она движется вместе с этой осью, а значит, покоится относительно этой оси. Другие точки на оси будут получать тем большую пространственную часть, чем дальше они находятся от исследуемой точки. А по временной составляющей 4-скорости темп времени падает, тем больше, чем дальше она находится от исследуемой точки. Итак, делаем вывод: галактики в двух противоположных направлениях, в которые упирается эта ось-плоскость, будут иметь поперечное красное смещение из-за пространственно-временного поворота по координате z.
Поскольку другая ось-плоскость вращается в перпендикулярном направлении, то там тоже будет наблюдаться поперечное красное смещение, но там оно обусловлено поперечным движением в плоскости (x,y).
Такое вращение объясняет очень много вещей:
наличие спина у каждой частицы;
наличие квантовой ψ-функции;
право-левая асимметрия в спиральностях галактик;
почему условный возраст Вселенной 13,34 млрд. лет, всегда!
аномально быстрое вращение периферийных частей галактик;
критическая плотность Вселенной может быть меньше...
Если скорости вращения вдоль осей чуть-чуть отличаются, то мы можем увидеть мультипольную структуру в реликтовом фоне, и небольшую анизотропию в красных смещения галактик.
Мировые линии.
На gif-анимированном рисунке мы видим движение шаров. На самом деле воображаемую картину необходимо несколько усложнить, вообразив мировые линии галактик. Для галактик, вращающихся в плоскости (z,ict), время мы отождествляем с цветом. Если время с этой стороны рисунка идет в одном направлении, то с противоположной стороны рисунка время идет вспять. Этому не стоит удивляться. Как известно, такое уже в физике встречалось, - позитрон это электрон, живущий вспять во времени. А на страницах о квантуемой скорости, мы развили эту идею и увидели, что каждая элементарная частица живет во времени "туда-сюда".
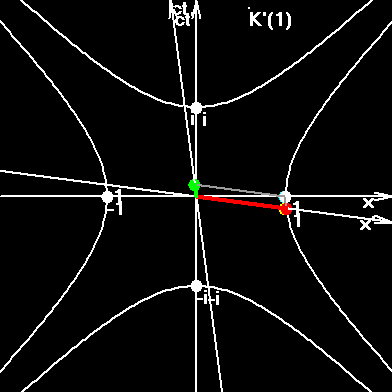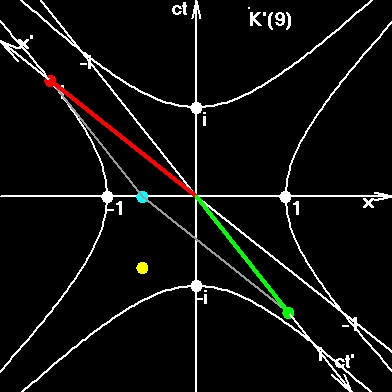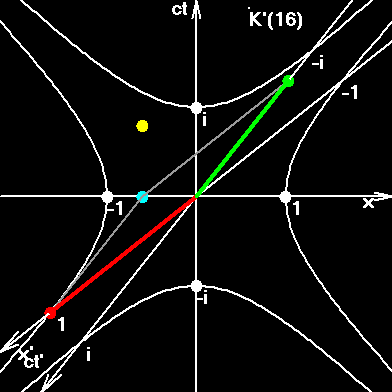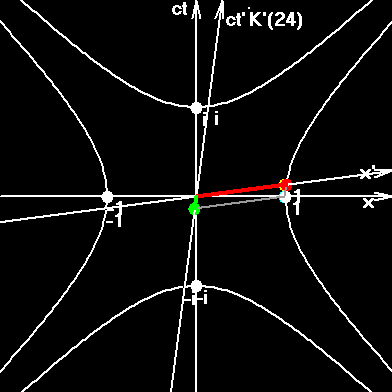
Составная частица "вспыхивает" в моменты стыковок квазизамкнутых окружностей. И, если по завершению обхода, какая-то из элементарных частиц опаздывает или опережает другие частицы, то в момент пространственно-временной синхронизации она получает элементарное изменение скорости, или другими словами - совершает элементарный поворот в пространстве-времени.
Такие же элементарные повороты в пространстве-времени мы увидим если проследим за движением шаров на нашем вращающимся рисунке, дополненным другим рисунком.
Вселенная Компьютерный
рисунок jpg, 116 кб.

Совершим элементарный переход из центра этого рисунка в любую сторону. При этом она окажемся ближе к какой-то условной границе. Но поскольку Вселенная изотропна и однородна, мы должны выполнить преобразования с другими галактиками, - переместить их так, чтобы исследуемая частица оказалась снова в центре.
Мысленно выполняя эту процедуру, замечаем, что галактики, которые были сзади у дальней границы, после преобразования окажутся у передней границы.
Если перемещение совершается вдоль временной компоненты, то галактики, которые находились у горизонта событий в прошлом, исчезают и появляются в далеком будущем "сверху над световым конусом".
Галактики, которые находятся в пределах светового конуса в промежуточном положении между исследуемой перемещаемой галактикой и горизонтом событий, из-за серии последовательных преобразований получают скорость удаления, подобную той, которая "наблюдается" в расширяющейся модели Вселенной.
Помимо выхода вещества за пределы горизонта событий в далеком прошлом, а соответственно, процесса уменьшения концентрации частиц в связи с ускорением удаления галактик, существует процесс, компенсирующий число галактик в пределах светового конуса.
Число галактик понятие относительное. Около нашей Галактики существуют спутники, БМО и ММО. Вполне возможно, что сейчас зарождаются и другие спутники, - от Галактики отделяются какие-нибудь скопления звезд. Со временем это будут независимые галактики с большим числом звезд. Вопрос, - откуда берется материя.
Во-первых, - вхождение вещества в световой конус сверху. Во-вторых, - гамма-всплески. Этот процесс изложен на странице Модель Хойла и 4d вращение. Оказывается, что четырехмерное вращение Вселенной в двух взаимно перпендикулярных плоскостях не только соответствует наблюдениям, но и реанимирует Стационарную модель Вселенной, созданную Фредом Хойлом, Германом Бонди и Томасом Голдом.
Некоторые полезные приложения из других источников.
Kissing Number
[3] Problems of arranging balls densely arise in many situations, particularly in coding theory (the balls are formed by the sets of inputs that the error-correction would map into a single codeword).
The most important question in this area is Kepler's problem: what is the most dense packing of spheres in space? The answer is obvious to anyone who has seen grapefruit stacked in a grocery store, but a proof remains elusive. (It is known, however, that the usual grapefruit packing is the densest packing in which the sphere centers form a lattice.)
The colorfully named "kissing number problem" refers to the local density of packings: how many balls can touch another ball? This can itself be viewed as a version of Kepler's problem for spherical rather than Euclidean geometry.
[1] In mathematics, sphere packing problems concern arrangements of non-overlapping identical spheres which fill a space. Usually the space involved is three-dimensional Euclidean space. However, sphere packing problems can be generalised to two dimensional space (where the "spheres" are circles), to n-dimensional space (where the "spheres" are hyperspheres) and to non-Euclidean spaces such as hyperbolic space.
A regular arrangement (also called a periodic or lattice arrangement) is one in which the centres of the spheres form a very symmetric pattern called a lattice. Arrangements in which the spheres are not arranged in a lattice are called irregular or aperiodic arrangements. Regular arrangements are easier to handle than irregular ones—their high degree of symmetry makes it easier to classify them and to measure their densities.[2] The number of equivalent hyperspheres in dimensions n which can touch an equivalent hypersphere without any intersections, also sometimes called the Newton number, contact number, coordination number, or ligancy.
Exact values for lattice packings are known for n=1 to 9 and n=24 (Conway and Sloane 1993, Sloane and Nebe). Odlyzko and Sloane (1979) found the exact value for 24-D.
Exact values for general packings are known for n=1, 2, 3, 4, 8, and 24. Musin developed a bounding method in 2003 to prove the 24-dimensional case, and his method also provides proofs for three and four dimensions (Pfender and Ziegler 2004).
SO(4)
[4] In mathematics, SO(4) is the four-dimensional rotation group; that is, the group of rotations about a fixed point in four-dimensional Euclidean space. The name comes from the fact that it is (isomorphic to) the special orthogonal group of order 4.
Simple rotations
A simple rotation R about a rotation centre O leaves an entire plane A through O (axis-plane) pointwise invariant...
Half-lines from O in the axis-plane A are not displaced; half-lines from O orthogonal to A are displaced through α; all other half-lines are displaced through an angle < α.
Double rotations
A double rotation R about a rotation centre O leaves only O invariant. Any double rotation has at least one pair of completely orthogonal planes A and B through O that are invariant as a whole, i.e. rotated in themselves. In general the rotation angles α in plane A and β in plane B are different. In that case A and B are the only pair of invariant planes, and half-lines from O in A, B are displaced through α, β, and half-lines from O not in A or B are displaced through angles strictly between α and β.Isoclinic rotations
If the rotation angles of a double rotation are equal then there are infinitely many invariant planes instead of just two, and all half-lines from O are displaced through the same angle. Such rotations are called isoclinic or equiangular rotations, or Clifford displacements. Beware: not all planes through O are invariant under isoclinic rotations; only planes that are spanned by a half-line and the corresponding displaced half-line are invariant.
Ссылки на внешние источники:
1.
2.
3.
4.
К странице Четырёхмерный
Мир
К другим разделам Космической Генетики
darkenergy@yandex.ru Иван Горелик